Notes
three regular hexagons and a semi-circle solution
Solution to the Three Regular Hexagons and a Semi-Circle Puzzle
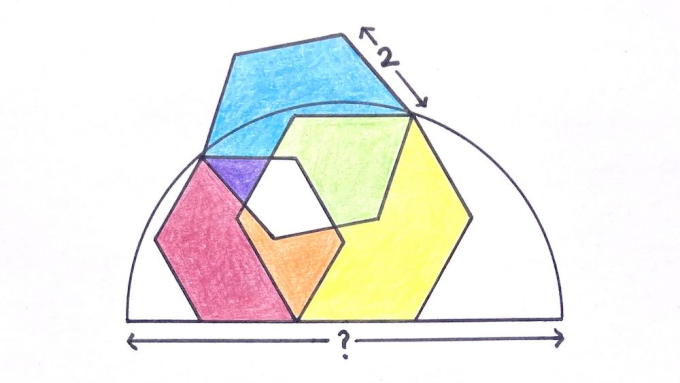
Three regular hexagons. What’s the diameter of the semicircle?
Solution by Properties of a Regular Hexagon and Angle at the Centre is Twice the Angle at the Circumference
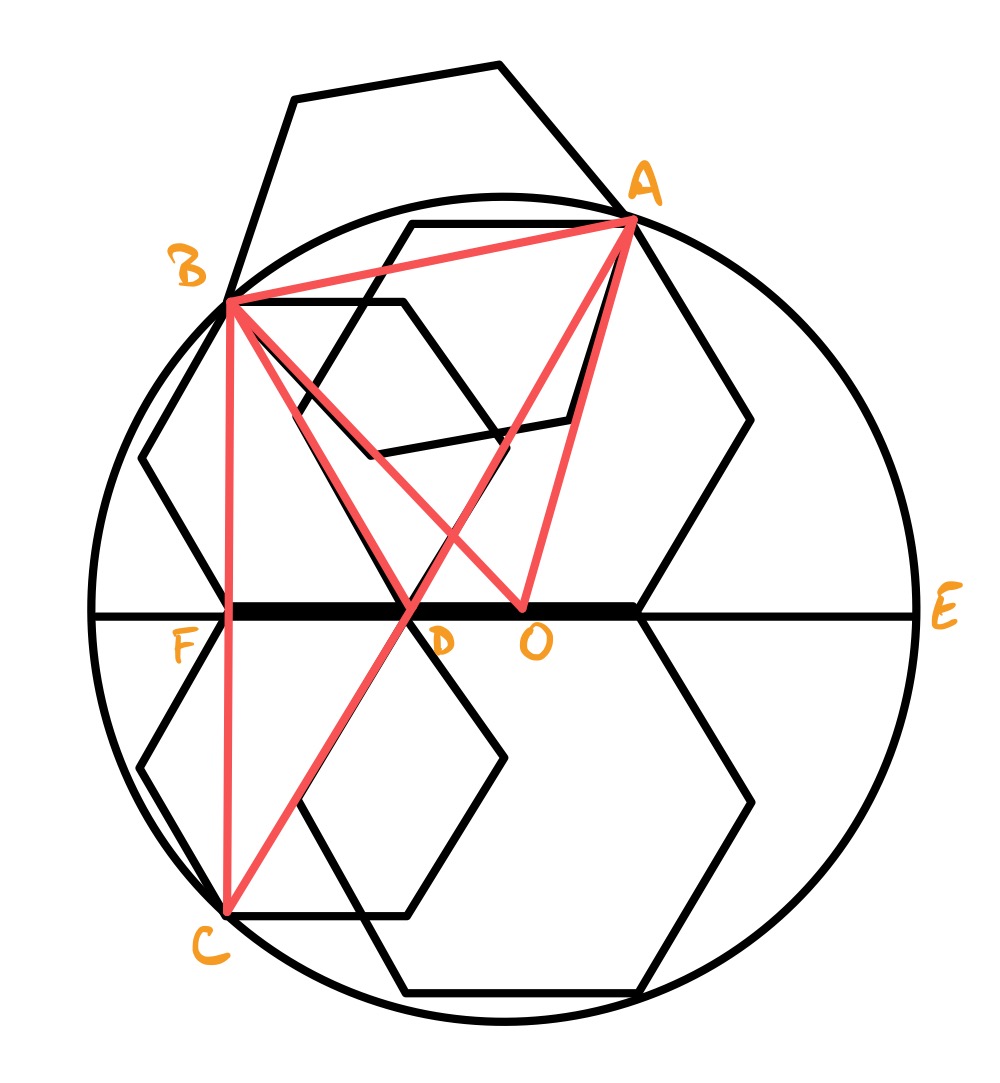
In the above diagram, the original semi-circle is extended to a full circle and the hexagons inside the semi-circle are reflected into the lower half. The point labelled is the centre of the circle.
Using angles in a regular hexagon, angle is , as is angle . Therefore, angle is also and so is a straight line.
Then is also a straight line, and angle is , so angle is also . Then since the angle at the centre is twice the angle at the circumference, angle is . So triangle is an isosceles triangle with one angle , hence is actually equilateral.
The radius of the semi-circle is therefore the same as the diameter of the hexagon, which is twice the side length, hene is $4.