Notes
three overlapping hexagons solution

Solution to the Three Overlapping Hexagons Puzzle

Solution by Properties of a Regular Hexagon

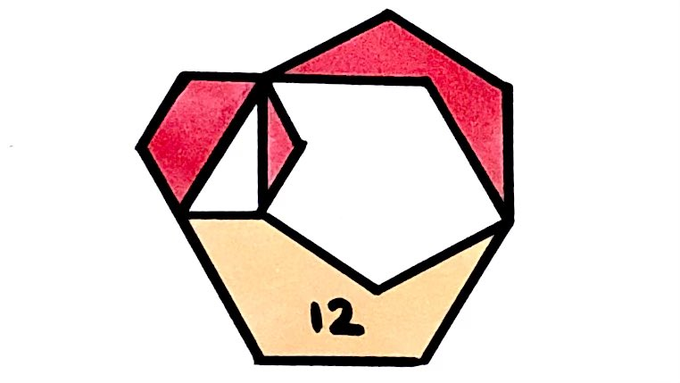
In the above diagram, the diagonal of the smallest hexagon is the same length as the side of the largest. From lengths in a regular hexagon, this means that the side length of the smallest hexagon is half that of the largest, so its total area is one quarter that of the largest.

The upper right red region can be dissected by extending the sides of the largest hexagon. Region $A$ fits into the smallest hexagon to fill it, while region $C$ is congruent to region $A$ and region $B$ can be moved to the right of $C$ to show that $B$ and $C$ have the same area as half the smallest hexagon. Therefore the area of the red region is $\frac{3}{2}$ of the smallest hexagon, so is $\frac{3}{8}$ of the largest.

The regions $B$ and $C$ also fit into the divot of the yellow region, completing that to half the largest hexagon. The regions $B$ and $C$ are, from above, in area half the smallest hexagon, which is a quarter the are of the largest. So $B$ and $C$, and hence the divot from the yellow region, is $\frac{1}{8}$th of the area of the largest hexagon.

The yellow region therefore comprises $\frac{1}{2} - \frac{1}{8} = \frac{3}{8}$ of the largest hexagon.

Therefore the red region has area $12$.

Solution by Dissection

In the above diagram, the red regions can be dissected and rearranged to fit exactly into the yellow region as indicated.