Notes
three hexagons in a trapezium solution
Solution to the Three Hexagons in a Trapezium Puzzle
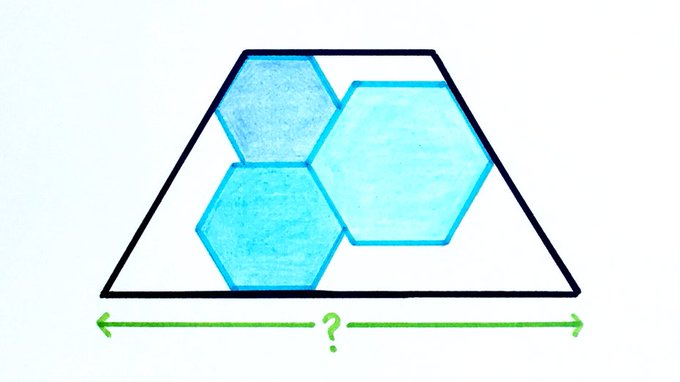
The perimeters of the regular hexagons add up to . How wide is the trapezium?
Solution by Congruency and Lengths in a Regular Hexagon
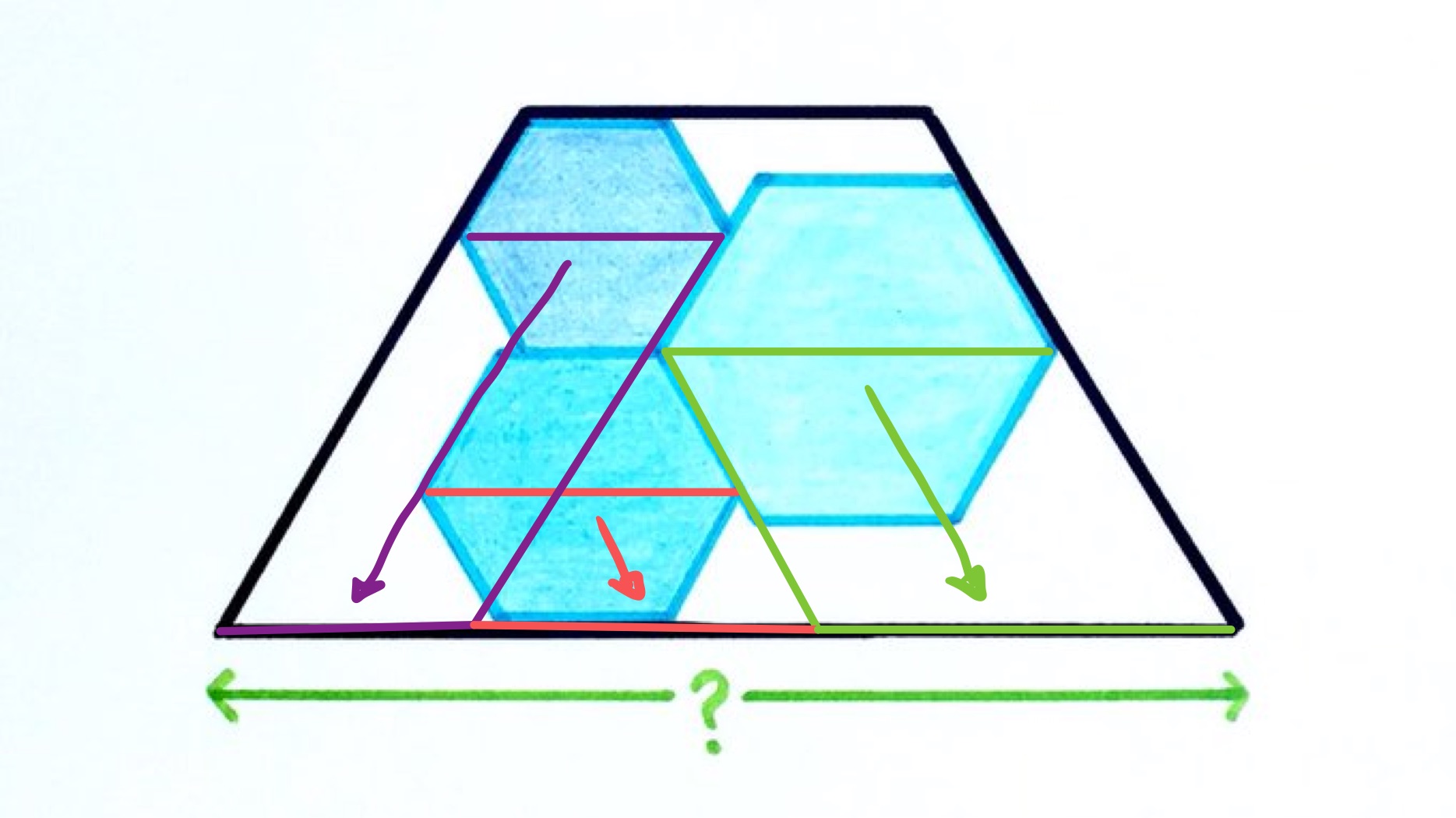
By sliding the lines as indicated in the above diagram, the base of the trapezium is seen to be formed from the diameters of the three hexagons. The diameter of a hexagon is twice its side length, while the perimeter of a hexagon is six times its side length. Therefore the base of the trapezium is a third of the perimeters of the hexagons, so is .
Solution by Invariance Principle
There are two special cases of this diagram. In the first all three hexagons are the same size. This means that the pattern can be extended to a tiling which shows that the base of the trapezium is three diameters.
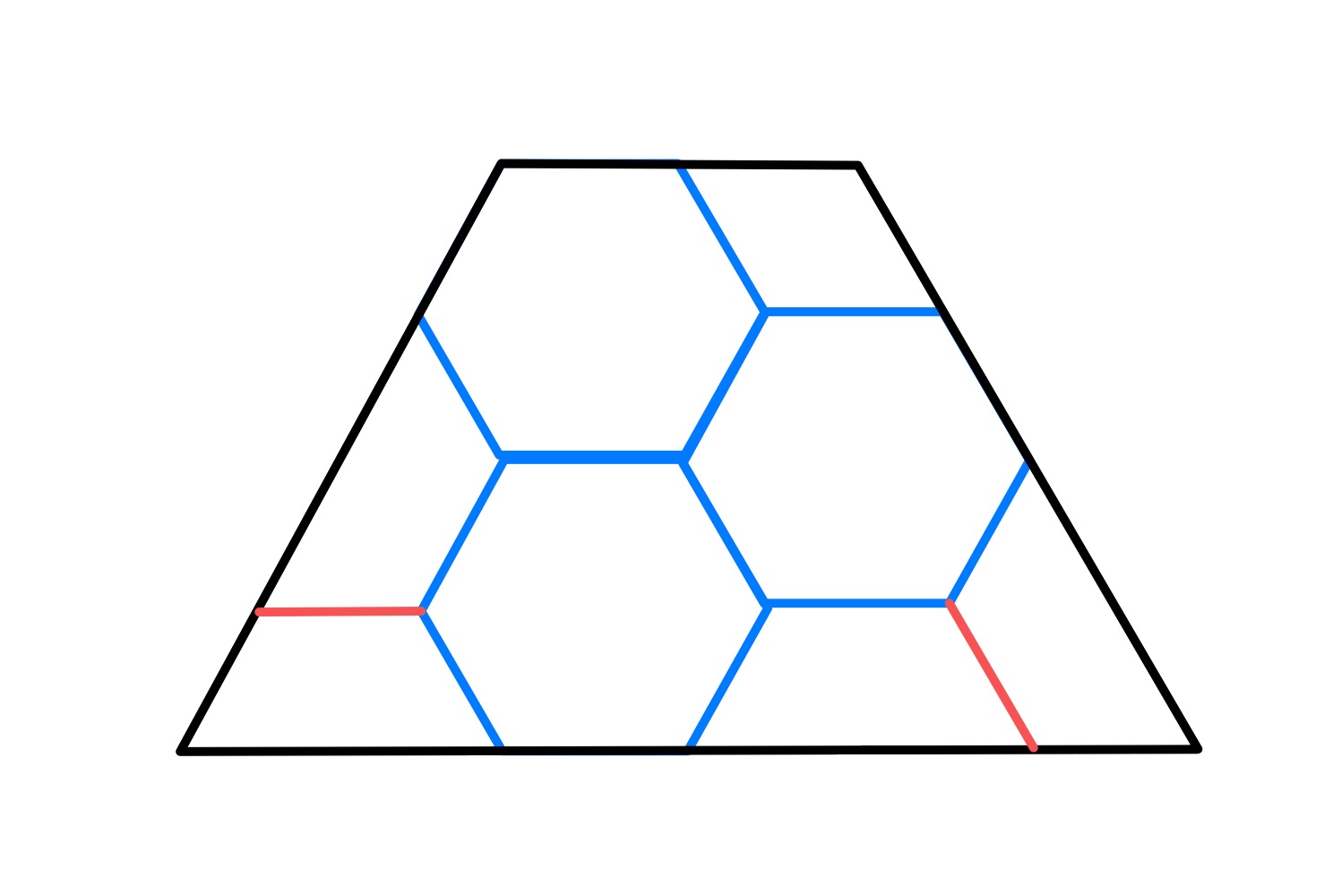
In the second, the large hexagon is twice the size of the smaller (which are themselves the same size). Tiling by the smaller hexagons shows that the base is again the sum of the diameters of the hexagons.