Notes
three hexagons and a rectangle solution
Solution to the Three Hexagons and a Rectangle Puzzle
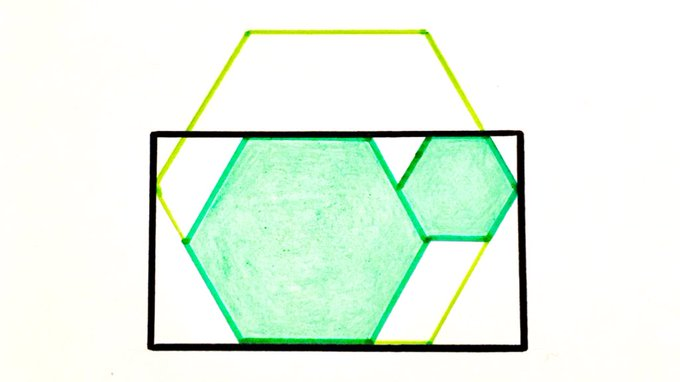
These hexagons are all regular. What fraction of the rectangle is shaded?
Solution by Properties of Hexagons
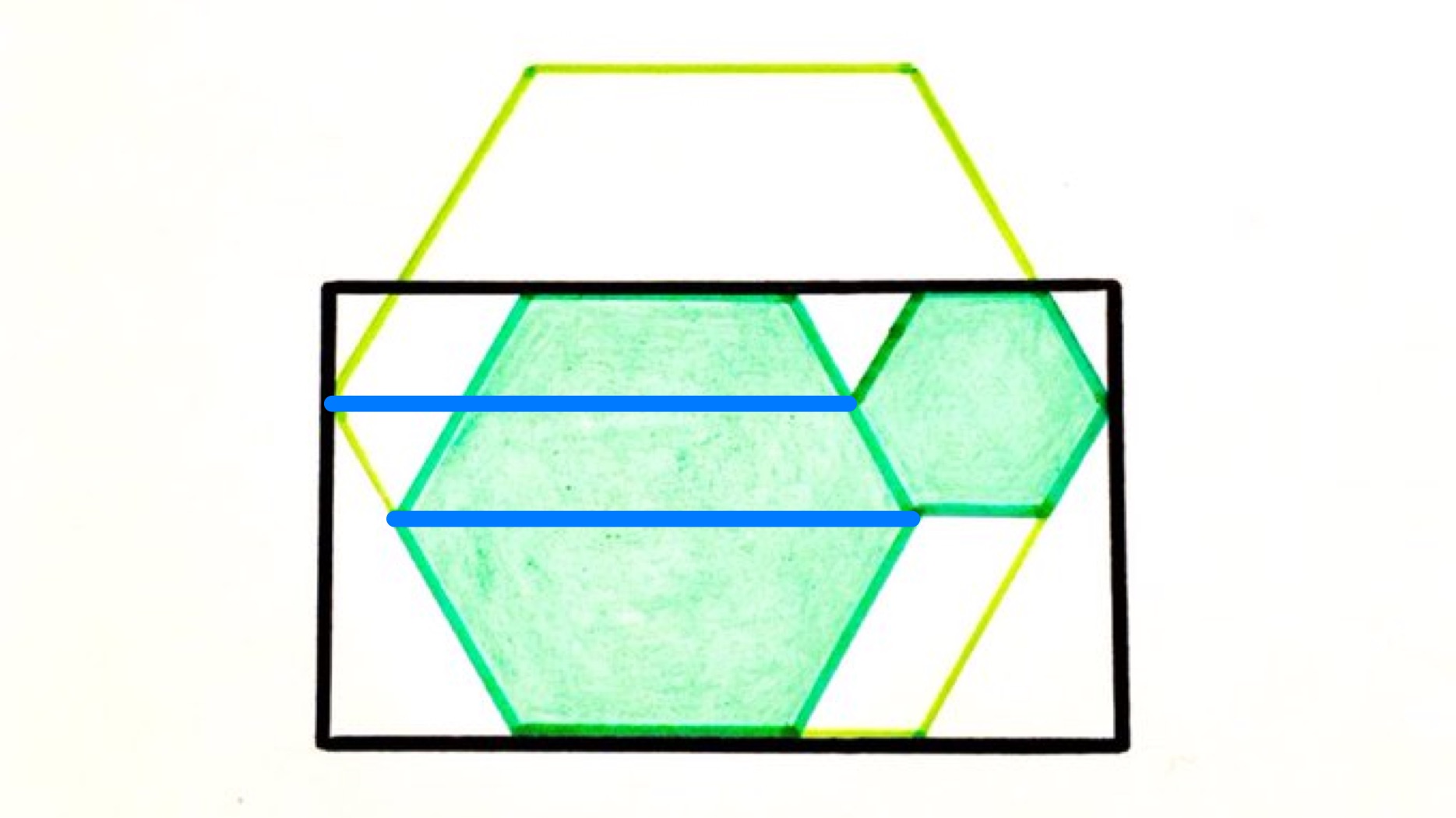
The smallest green hexagon can be seen to be half the height of the larger green one. The two blue lines show that by sliding the larger green hexagon to the left, the following diagram is obtained, wherein the right-most vertex of the larger green hexagon lines up with the left-most vertex of the smaller one.
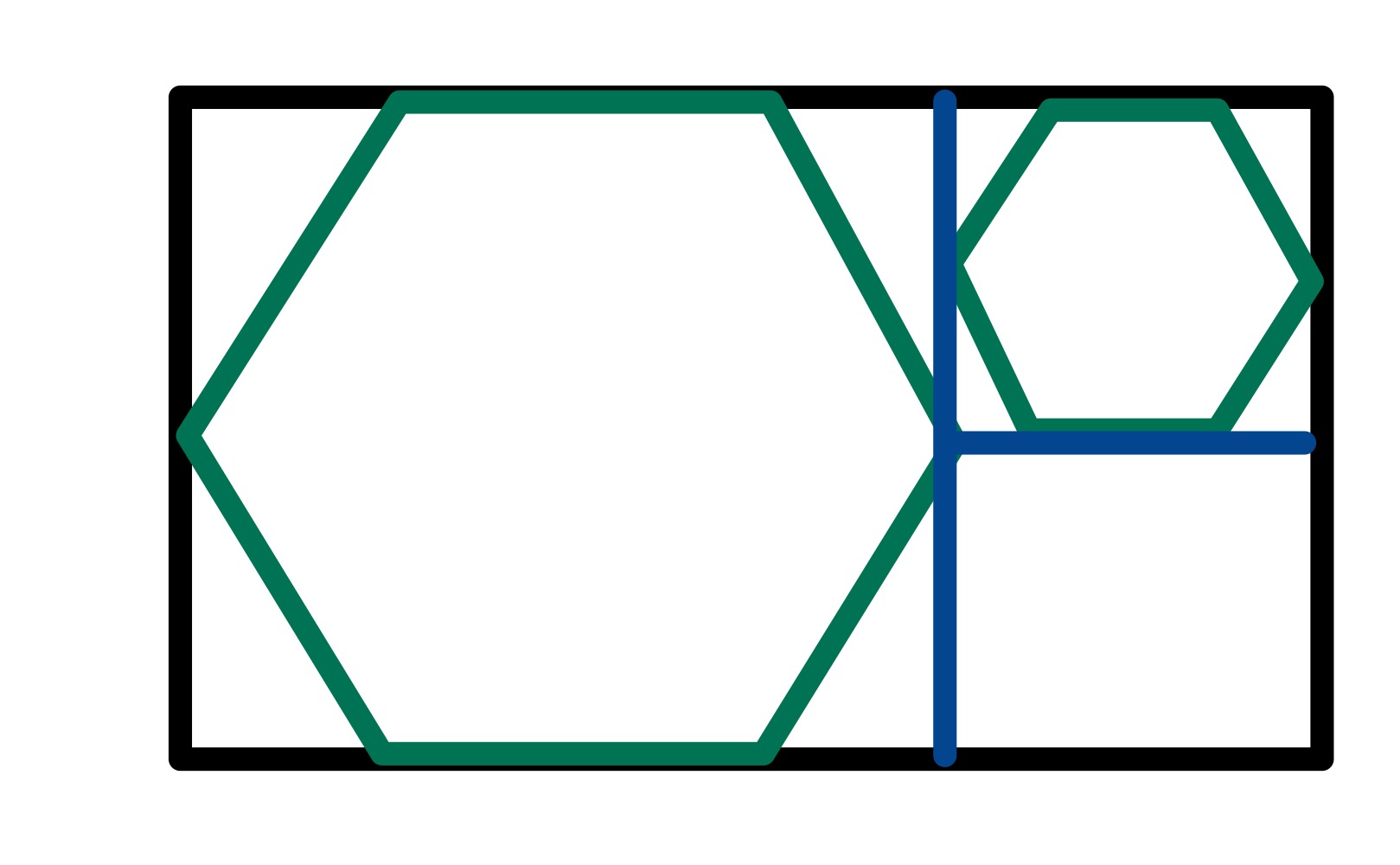
Considering just one hexagon with its surrounding rectangle, the excess outside the hexagon consists of three triangles, each of which is half of an equilateral triangle. Therefore the rectangle comprises eight equilateral triangles of which the hexagon is six.
As the smaller hexagon is half the height of the larger one, the equilateral triangles of the larger one are made from four of the smaller one. So thinking of each region in terms of the equilateral triangles of the smaller hexagon, the top right region has six of eight shaded, the lower right has all eight not shaded, and the left region has twenty-four of thirty-two shaded. This adds up to thirty shaded out of forty-eight in total, or a fraction of ths.