Notes
three congruent triangles solution
Solution to the Three Congruent Triangles
Posted on Oct 29, 2019
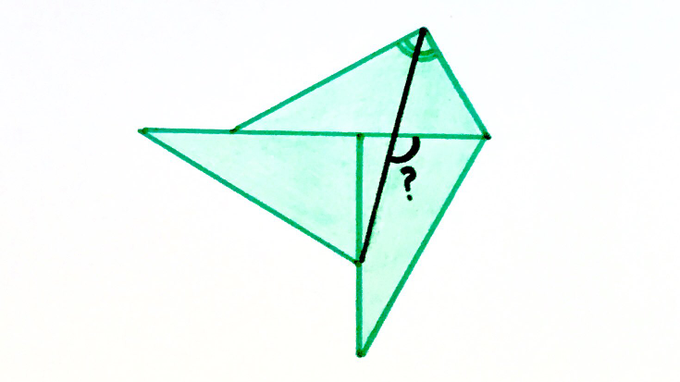
Three congruent triangles. The black line bisects the top angle. What angle does this line make with the horizontal?
Solution by Angle at the Centre is Twice the Angle at the Circumference, Equilateral Triangles, Angles in a Triangle
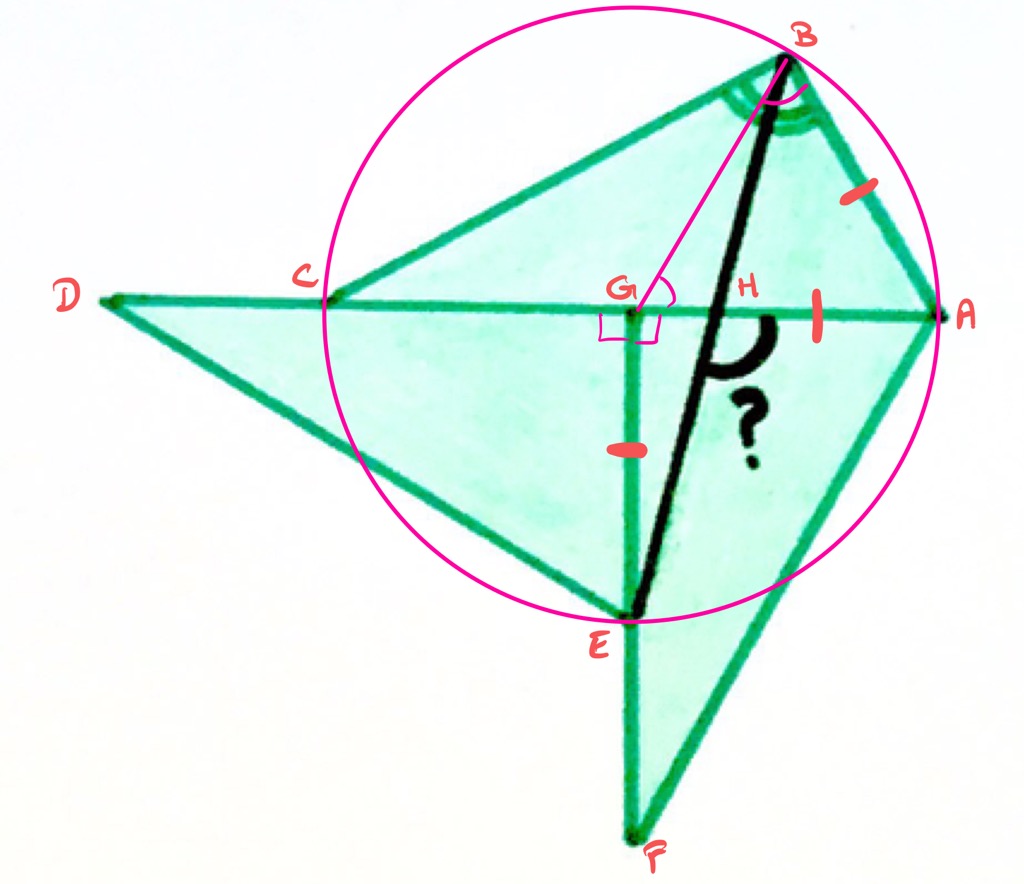
Let the points be labelled as above. Since the triangles are congruent, and is a straight line (as an edge of the upper triangle), angles and are both right-angles. Then angle is also a right-angle, and so since bisects angle , angle . Also, as the triangles are congruent, , , and all have the same length.
Draw a circle with centre that passes through . Then it must also pass through . Since angle is half of angle , by the converse to the result that the angle at the centre is twice the angle at the circumference, must lie on the circle. Therefore, has the same length as .
Since also has that same length, triangle is equilateral and so angle . Then since angle , angle and so angle .
Solution by Similar Triangles, Isosceles Triangles, and Vertically Opposite Angles
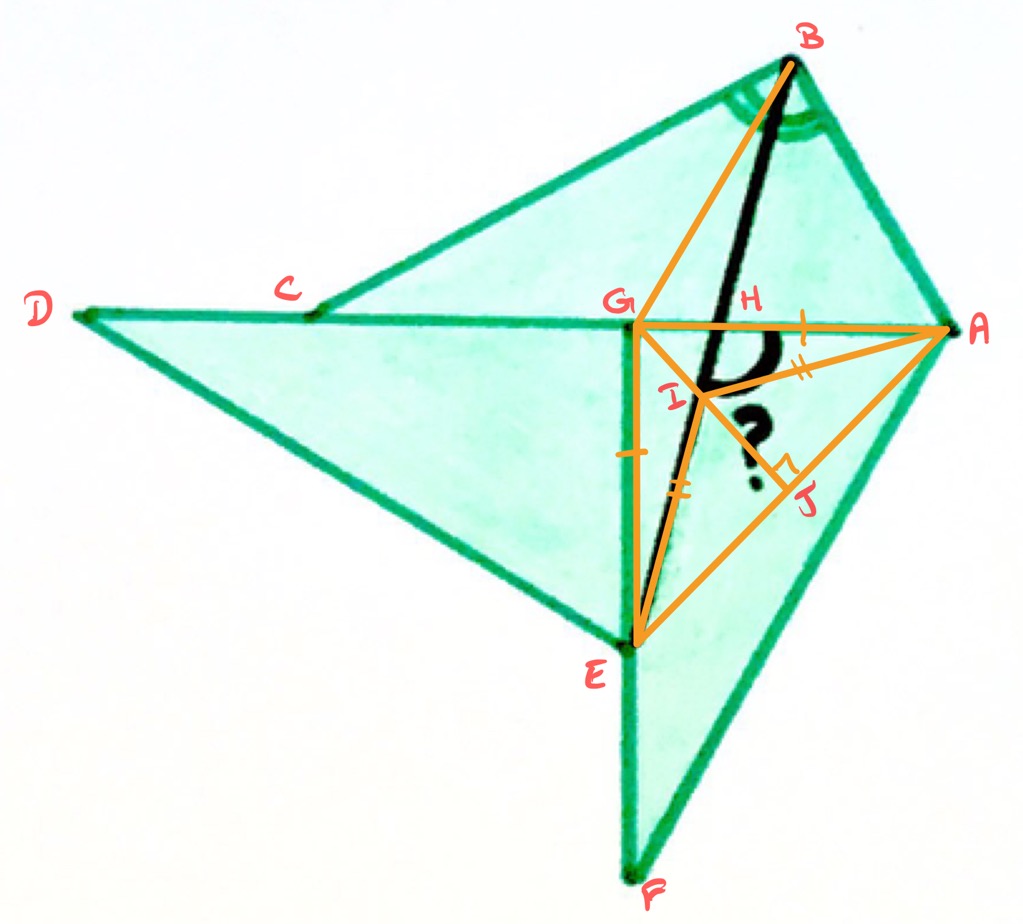
In the picture above, is the midpoint of , and is where meets . As in the previous argument, , , and all have the same length.
Since bisects angle , angle is equal to angle . Angles and are vertically opposite. Therefore triangles and are similar, with vertices corresponding as listed.
This means that the ratios of the lengths of and of are the same. Since also angles and are equal, triangles and are also similar. Therefore, angle is equal to angle . Then since both triangles and are isosceles, angles and are equal. Therefore, angles and are also equal. This means that triangle is also isosceles, and so has the same length as .
Therefore, triangle is equilateral. Then, as above, angle . Since angle , angle and so angle .