Notes
three congruent rectangles ii solution
Solution to the Three Congruent Rectangles II Puzzle
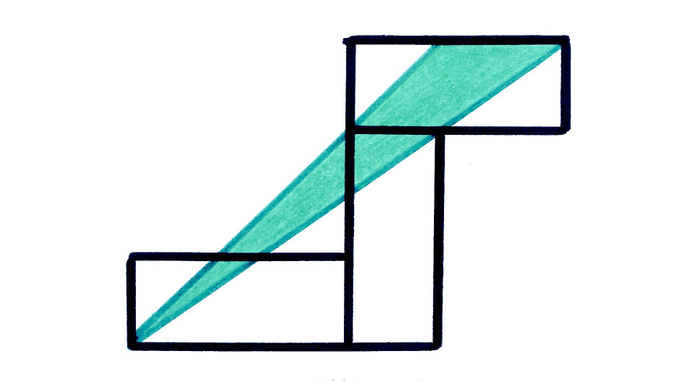
The rectangles are congruent, each with area . What’s the area of the triangle?
Solution by Similar Triangles and Area of a Triangle
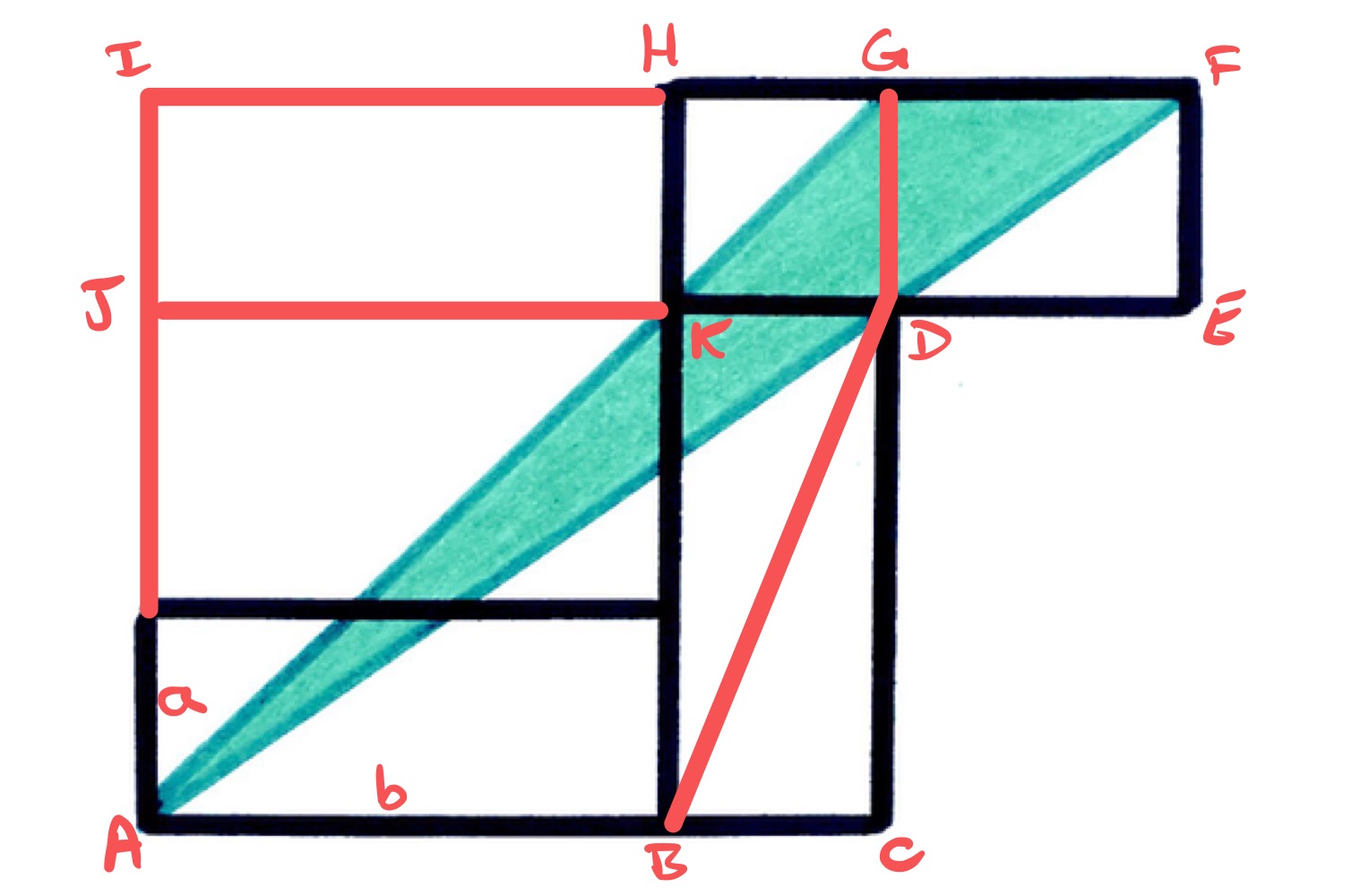
Consider the diagram labelled as above.
Since and are the same length, and is a straight line, by similar triangles then and are also the same length as each other. This means that is a square, and the area of triangle is half of that of .
Similarly, is a rectangle, and the area of triangle is half of that of it. Therefore, the area of trapezium is half that of rectangle .
Triangle can be viewed as having base , in which case its perpendicular height is the length of . This means that it has the same area as triangle , which is half of the area of .
In total, then, triangle has the same area as one of the congruent rectangles, namely .
Solution by Similar Triangles and Area of a Triangle
With the diagram labelled as above, let and be the lengths of the sides of the rectangles, with .
As the line passes through , triangles and are similar. The horizontal and vertical lengths of these triangles are, respectively, and for triangle and and for . Therefore:
The rectangles have area , so . This means that .
Triangles and are likewise similar, so since and have the same length, and are also the same length, which is . Therefore, has length .
The area of the shaded triangle is therefore: