Notes
subdivided semi-circle solution
Solution to the Subdivided Semi-Circle Puzzle
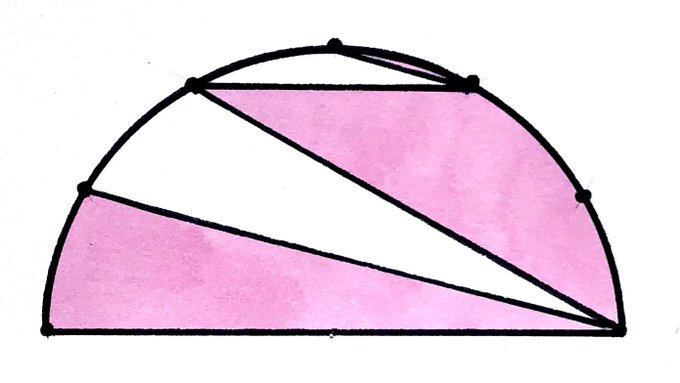
The dots around the circumference of this semicircle are equally spaced. What fraction is shaded?
Solution by Dissection, Lengths in a Regular Hexagon, and the Area of a Triangle
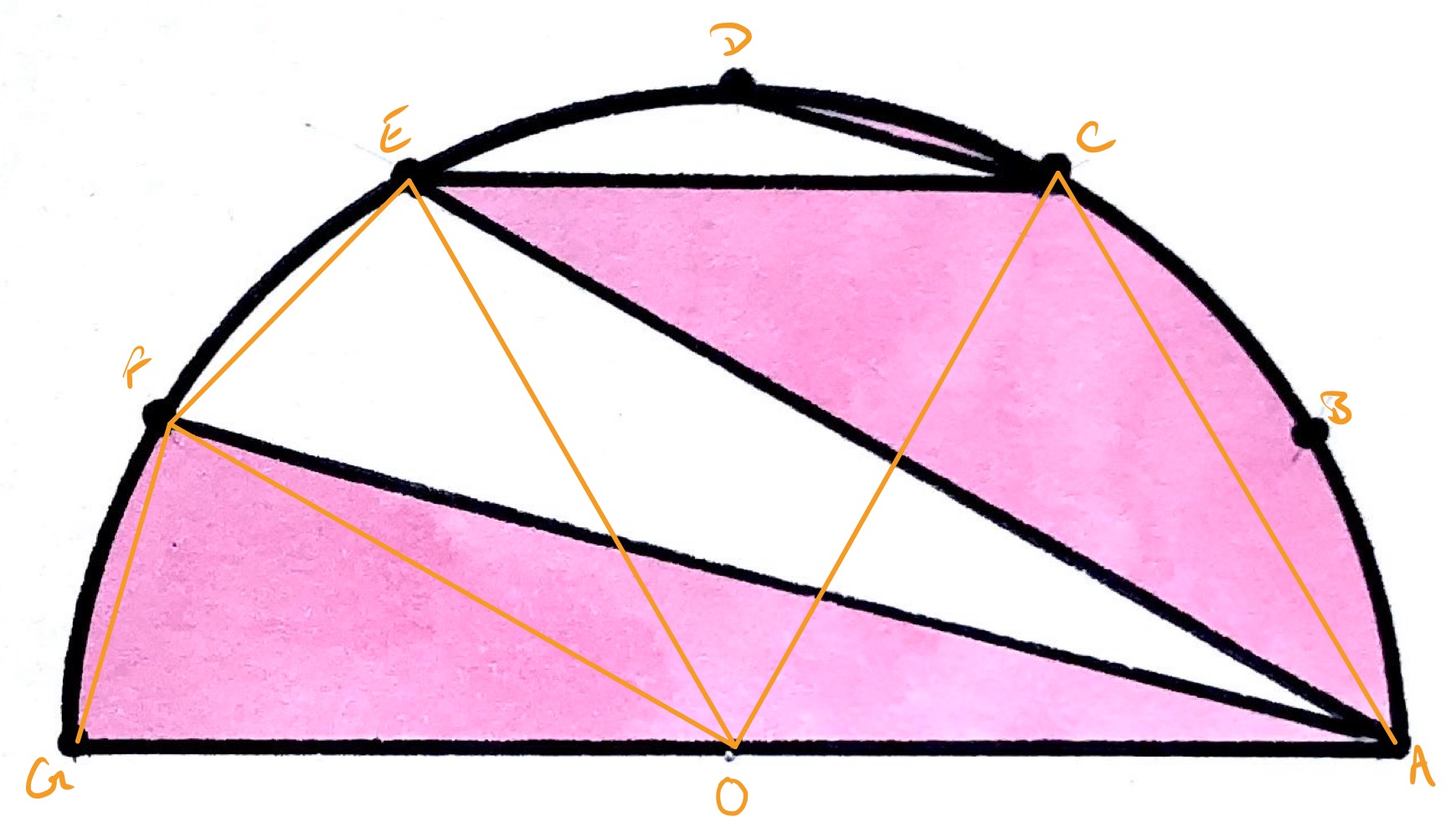
Label the points as in the diagram above, where is the centre of the semi-circle.
Consider the region formed by the arc and line segments and .
As the points are equally spaced around the semi-circle, points , , , and form part of a regular hexagon. Therefore, is parallel to . This means that triangles and have the same area as both have the same “height” above . The area of the region formed by the arc and line segments and is therefore the same as the area of the sector .
Consider the region formed by the arc and line segments and .
The two triangles and have the same length base, as they are both radii of the same circle, and the same height, as it is the height of above , so they have the same area. Therefore, the area of triangle is the same as that of triangle . So the region formed by the arc and line segments and has the same area as that formed by the arc and line segments , , and .
Lastly, the area of the segment cut off by line segment is the same as that cut off by line segment , so combining this with the region above produces the same area as sector .
In total, the shaded regions have the same area as two sectors of the semi-circle, so their combined area is rds of the total.