Notes
striped semi-circle solution

Solution to the Striped Semi-Circle Puzzle

Solution by Congruent Triangles, Lengths in Equilateral Triangles, and the Area of a Semi-Circle.

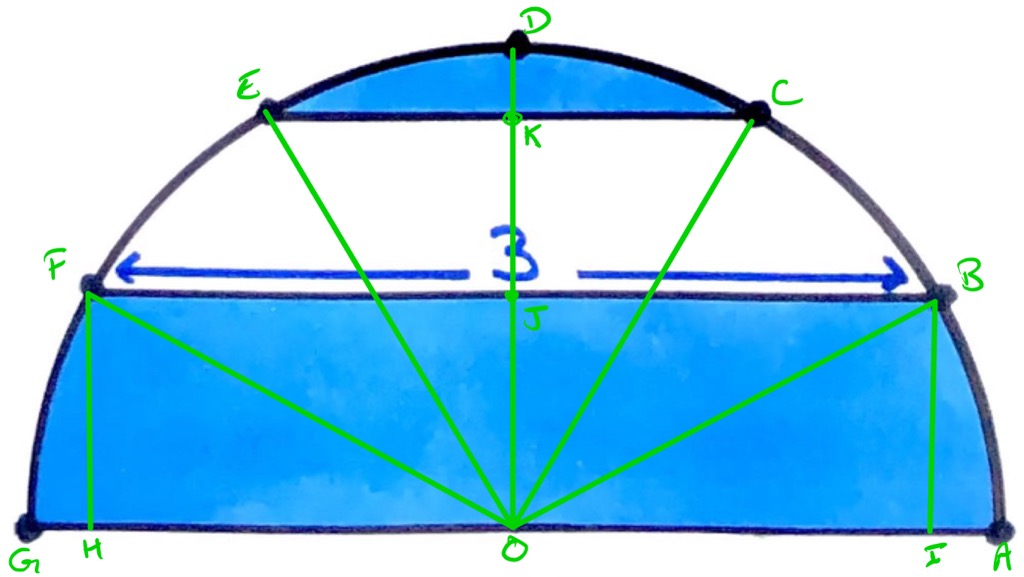
Consider the diagram as labelled above, in which $H$ and $I$ are such that angles $O \hat{H} F$ and $O \hat{I} B$ are right-angles. Then $H F J O$ is a rectangle, so triangles $J F O$ and $H O F$ are congruent. Triangles $H O F$ and $K O C$ are also congruent, so $J F O$ can be placed over $K O C$ to fill in sector $D O C$. Similarly, triangle $J B O$ can be placed over $K O E$ to fill in sector $D O E$. Therefore, the shaded region has the same area as four sectors. Its area is therefore $\frac{4}{6}$ths of the area of the semi-circle.

To find the area of the semi-circle, we need to find its radius. Triangle $J F O$ is right-angled and angle $F \hat{O} J$ is $\frac{2}{6}$ths of $180^\circ$, which is $60^\circ$. Therefore, triangle $J F O$ is half of an equilateral triangle which means that the length of $F J$ is $\frac{\sqrt{3}}{2}$ of the length of $O F$. Therefore, the length of $O F$ is $\frac{3}{2} \div \frac{\sqrt{3}}{2}$ = \sqrt{3}$.

The shaded region therefore has area: