Notes
six semi-circles inside a hexagon solution
Solution to the Six Semi-Circles Inside a Hexagon Puzzle
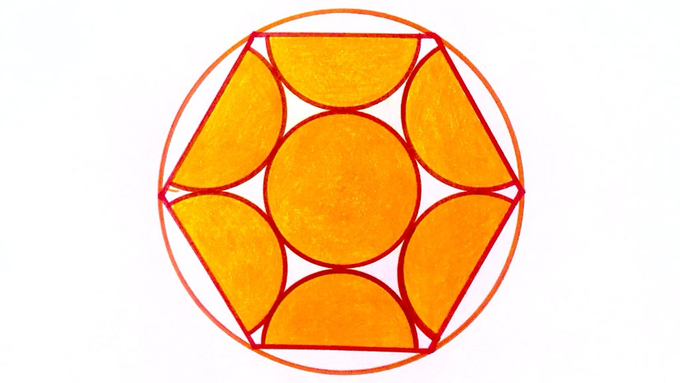
Six equal semicircles (and a circle) sitting in a regular hexagon. What fraction of the outer circle is shaded?
Solution by Lengths in a Regular Hexagon
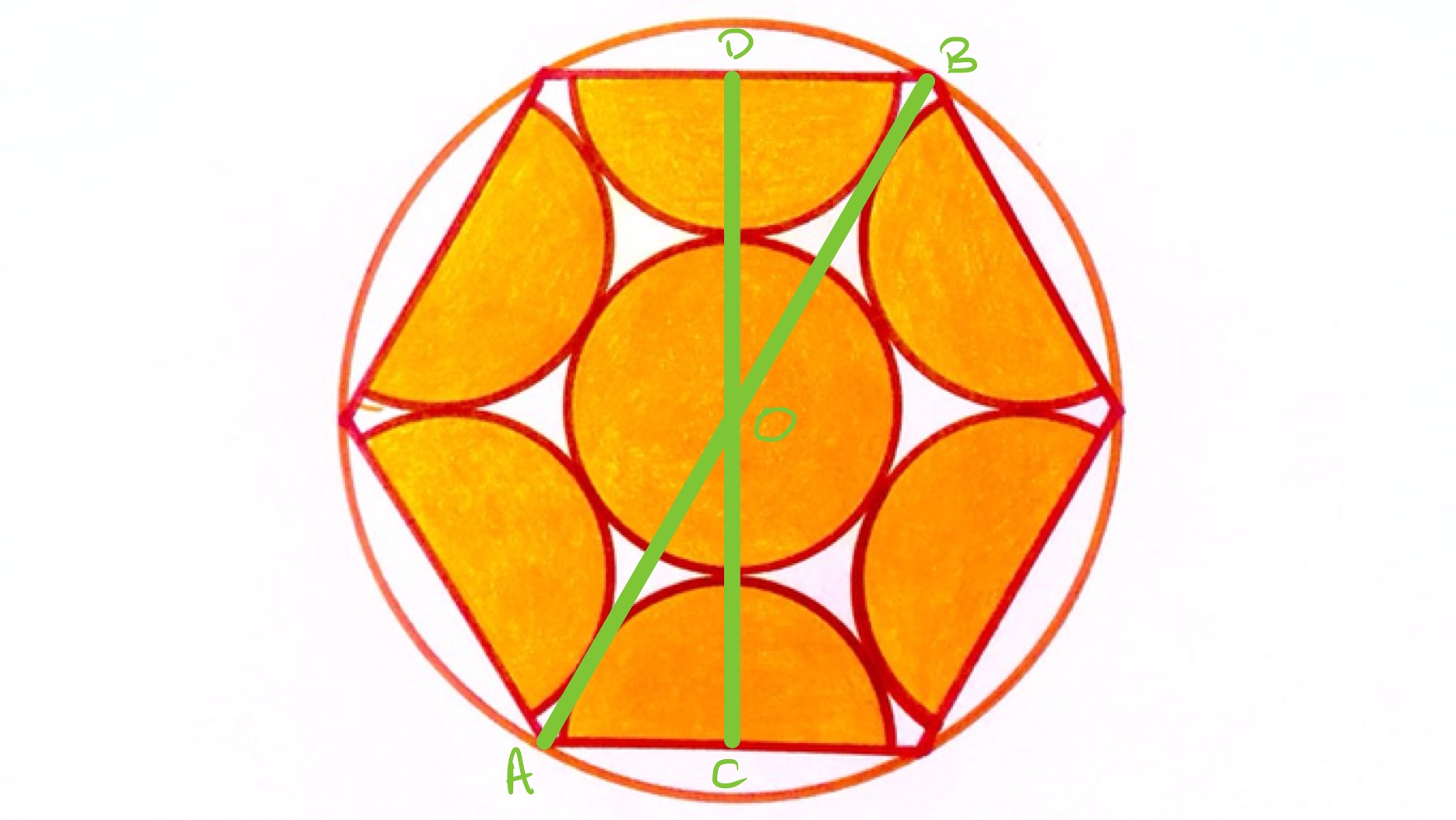
In the diagram above, the line segment is the diameter of the outer circle and the line segment is twice the diameter of the smaller circles. From the relationship between lengths in a regular hexagon, the length of is of the length of . Therefore the diameter of the outer circle is times the diameter of the inner circles. Its area is then times the area of one of the circles, as there are four complete small circles the area of the outer circle is times the shaded area and so the shaded area is of the outer circle.
(Note: the wording can be taken to imply directly that the central circle has the same radius as the semi-circles. If this is not taken as given it can be demonstrated by joining the midpoints of adjacent edges of the hexagon to each other and to the centre of the hexagon. This forms an equilateral triangle and from this the equality of the radii can be deduced.)