Notes
six equal area rectangles solution
Six Equal Area Rectangles
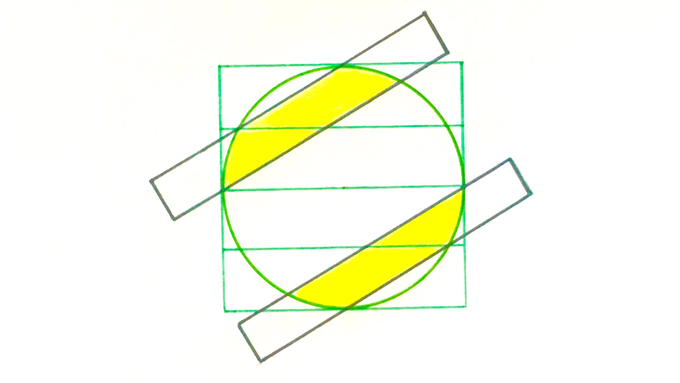
The six rectangles each have area . What’s the total shaded area?
Solution by Chord Properties, Equilateral Triangles, and Area of a Sector
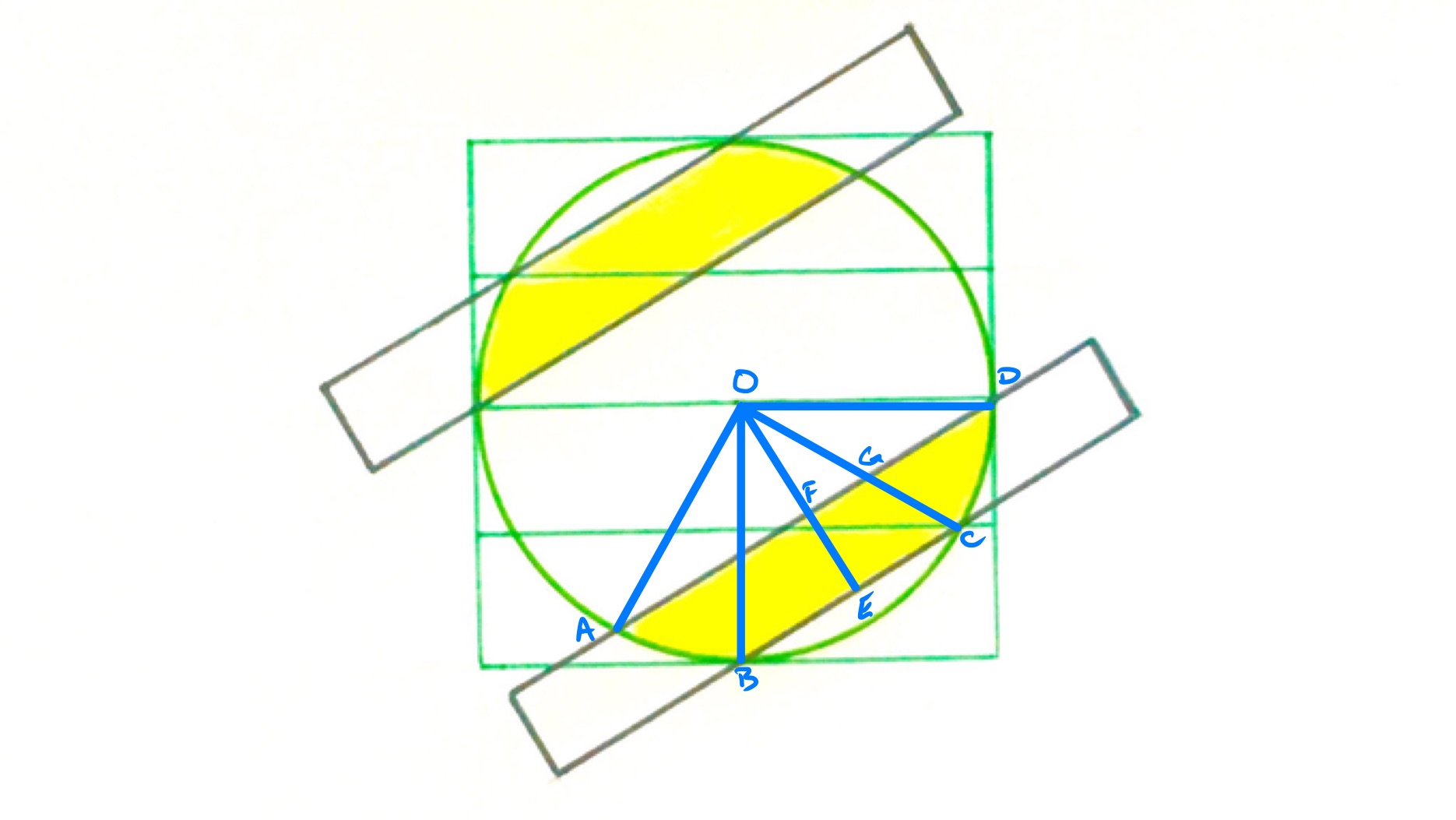
With the points labelled as in the above diagram, is the centre of the circle and the midpoint of . So also is the midpoint of . Let be the length of its radius.
The horizontal rectangles are all congruent, since they have the same width and area, so the height of two of them is a radius, or . Their width is twice the radius, so their area is . Hence .
In the right-angled triangle , the length of is half that of , and so this is half an equilateral triangle. In particular, angle is . So then angle is .
Since is the midpoint of the chord , angle is a right-angle. Angle is , and so triangle is also half an equilateral triangle. Since and have the same length, triangles and are congruent. As they overlap in triangle , this means that triangle and quadrilateral have the same area.
This then means that the region (with the arc) and the sector have the same area. The total yellow region comprises four congruent copies of , and so their area is the same as four sectors with central angle , equivalently one sector with central angle . Hence the yellow regions have total area: