Notes
shaded spikes in a hexagon solution
Solution to the Shaded Spikes in a Hexagon Puzzle
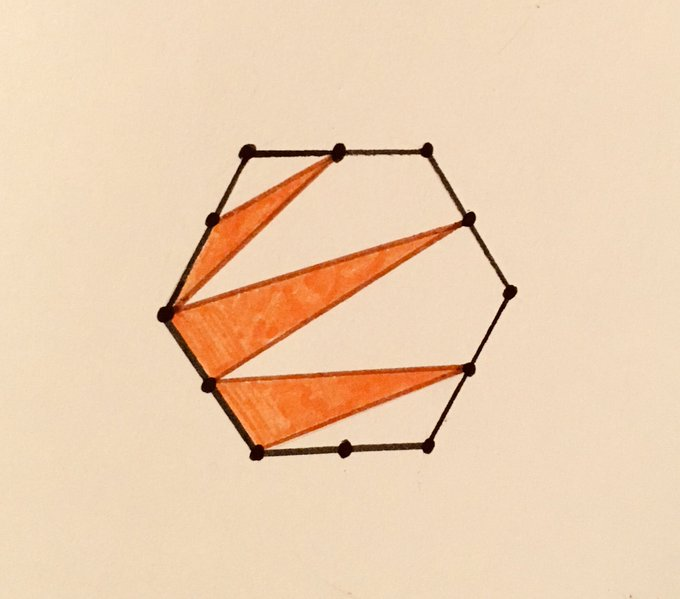
What fraction is shaded? The hexagon is regular, with equally spaced dots around its perimeter.
Solution by Properties of a Regular Hexagon and the Area of a Triangle
Consider the diagram labelled as below.
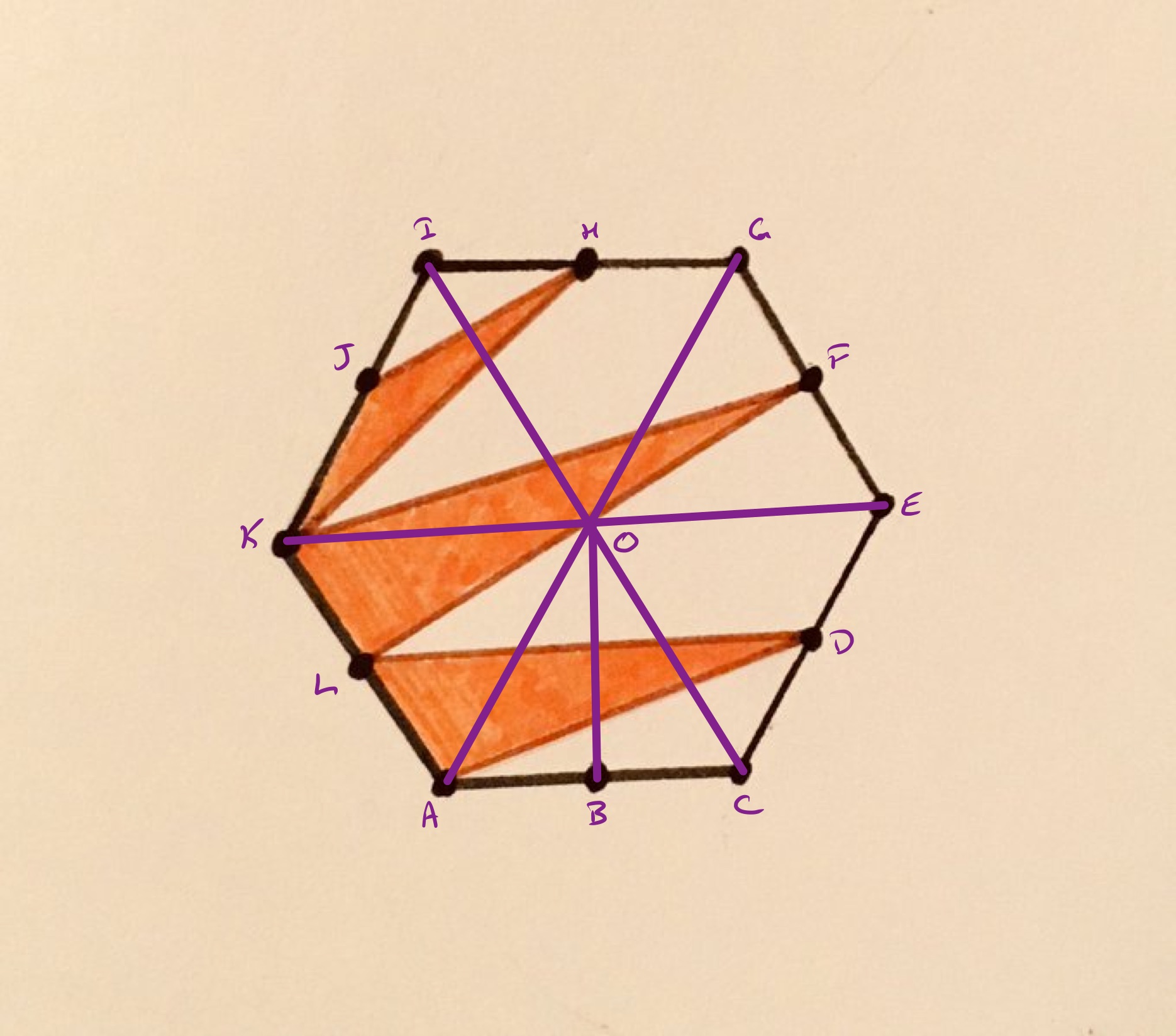
From the properties of a regular hexagon, the triangles with apex at and side one of those of the hexagon are all equilateral. Each has area th of that of the hexagon.
Let be the height of one equilateral triangle, so the length of , and let be the base, so the length of . Then the area of the hexagon is .
As the points and are the midpoints of their sides, the length of is half way between that of , namely , and of , namely . So has length . Similarly, the height of above the line is , so the area of triangle is .
The length of is and of is , so the area of triangle is .
The height of above is half of the height of (and of ) so is . Since has length this means that triangle has area .
The total shaded area is therefore:
Since the area of the hexagon is this means that one third of the hexagon is shaded.
Solution by Properties of a Regular Hexagon and Dissection
Consider the diagram labelled as below.
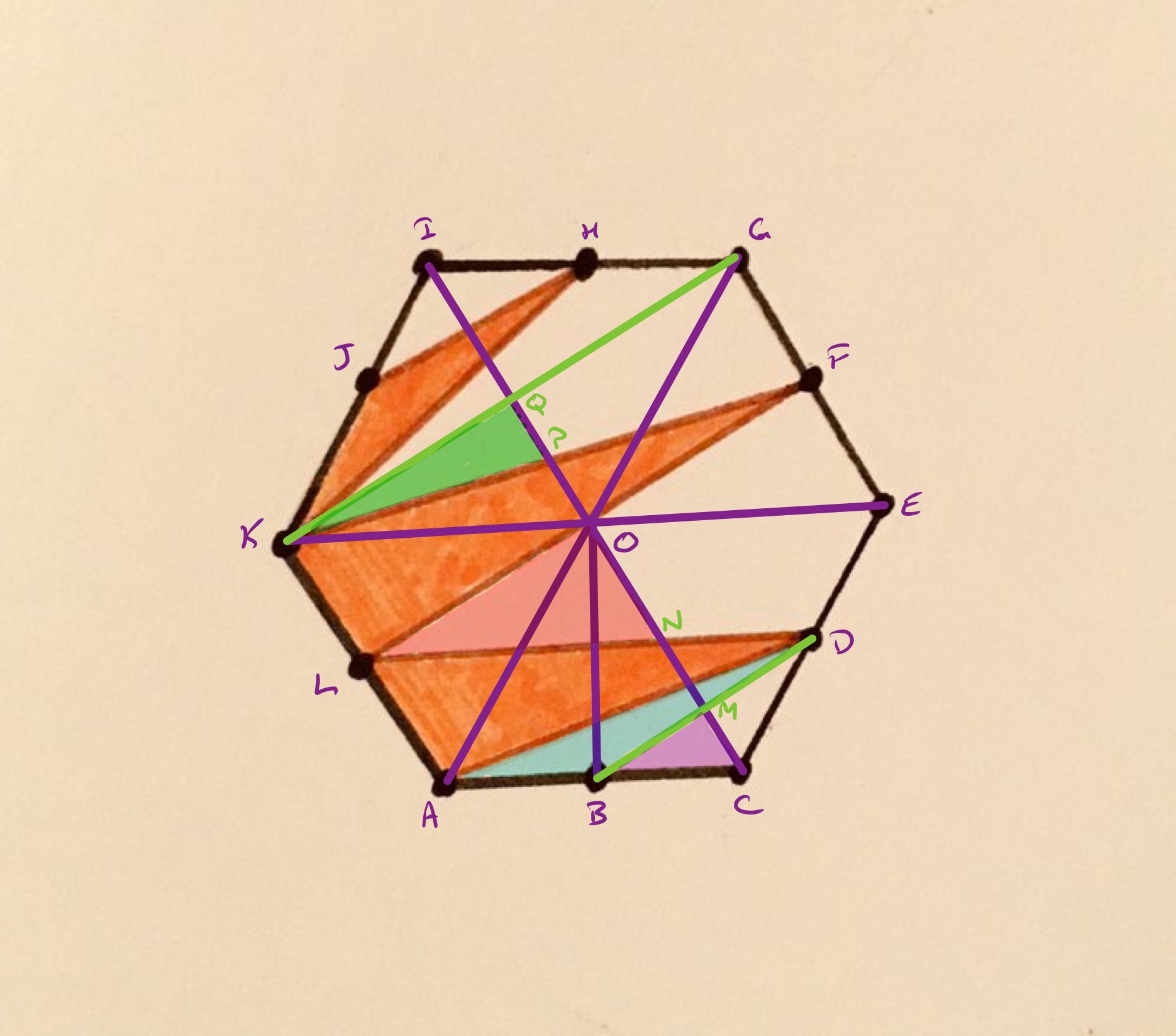
The (orange) shaded areas are cut and reassembled as follows.
- Triangle is flipped and translated to , where it fits exactly.
- Triangle is rotated round to fit in .
- Triangle is rotated round to fit in .
- Triangle is translated to fit in .
This leaves the shaded area being parallelogram which consists of two of the six equilateral triangles that make up the hexagon. The shaded area is therefore one third of the total.