Notes
polygons with equal perimeter solution
Polygons with Equal Perimeter
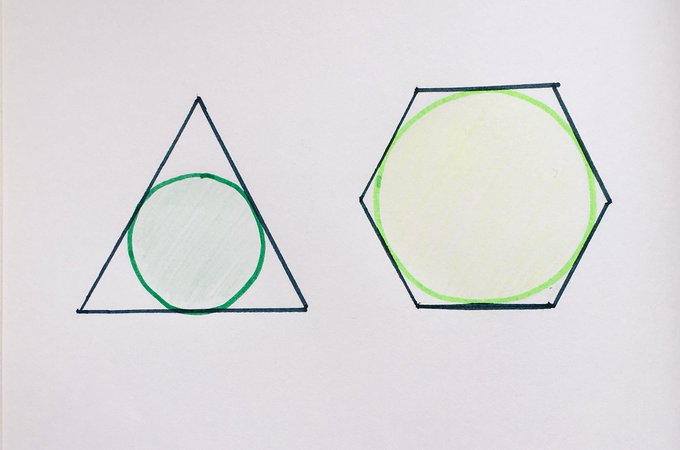
These regular polygons have the same perimeter. Find the ratio of the area of the circles.
Solution by Lengths in a Regular Hexagon and Lengths in an Equilateral Triangle
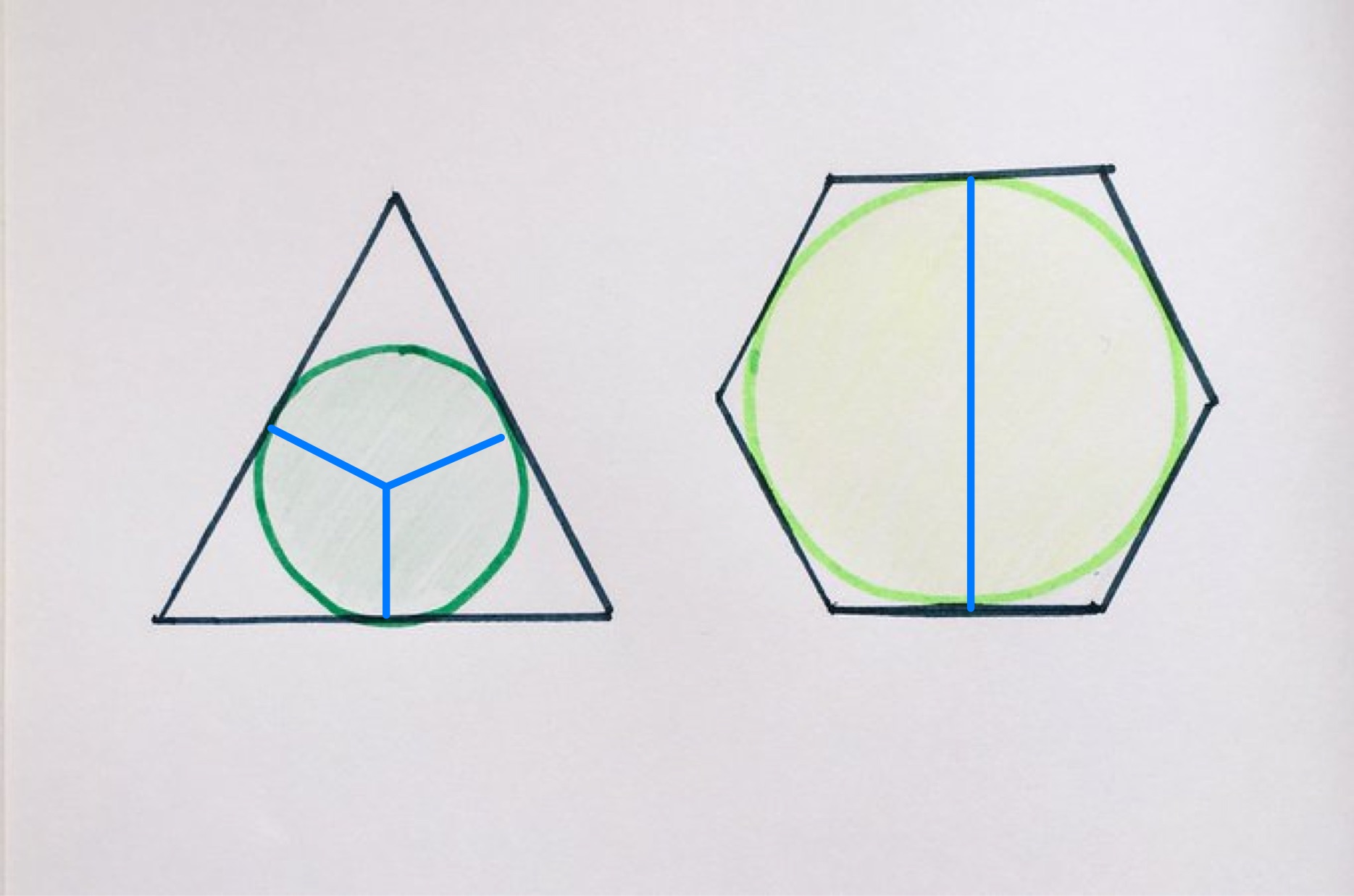
As the triangle and hexagon have the same perimeter, the side length of the hexagon is half that of the triangle. Let be the side length of the hexagon. From lengths in a regular hexagon, the height of the hexagon is . The area of the circle is therefore . From lengths in an equilateral triangle, the radius of the incircle is times the side length of the triangle, so is so its area is . The ratio of the area of the circles is therefore .