Notes
overlapping triangle and hexagon solution
Solution to the Overlapping Triangle and Hexagon Puzzle
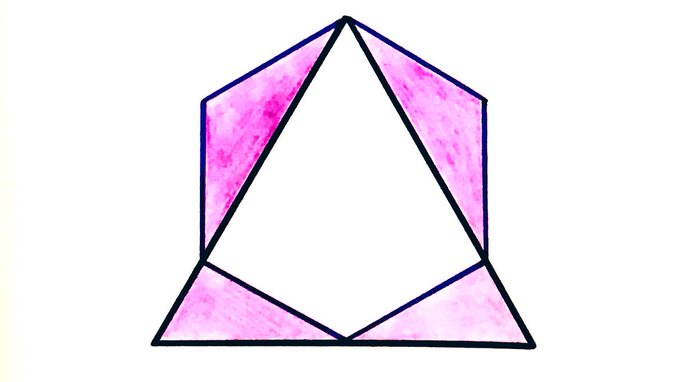
One corner of the regular hexagon is on the midpoint of the triangle’s base. What fraction of the total area is shaded?
Solution by Properties of Regular Hexagons and Equilateral Triangles
Let be the length of one side of the hexagon. Using lengths in a regular hexagon, the equilateral triangle has height and so has base . Its area is therefore . The two remaining parts of the hexagon each can be reassembled into an equilateral triangle with side length , so each has area . The total area is therefore:
The unshaded area consists of the hexagon without the two upper triangles, so has area equal to four equilateral triangles with side length . Its area is therefore . The shaded area is therefore
The fraction that is shaded is then .