Notes
nested circles and polygons solution

Skip the Navigation Links | Home Page | Feeds

Nested Circles and Polygons

Nested Circles and Polygons

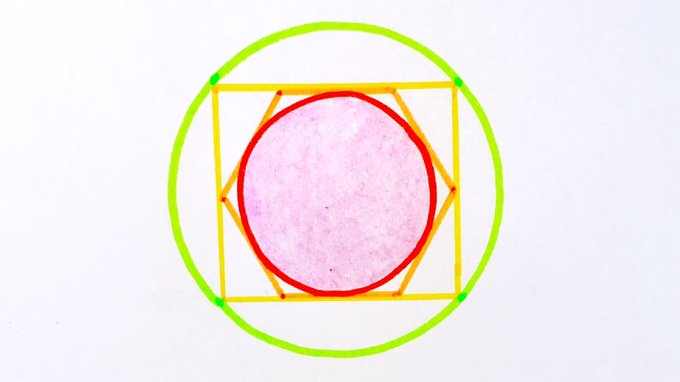
Two circles, a rectangle and a regular hexagon, all neatly packed inside each other. What fraction of the outer circle is shaded?

Solution by Properties of a Regular Hexagon and Pythagoras' Theorem

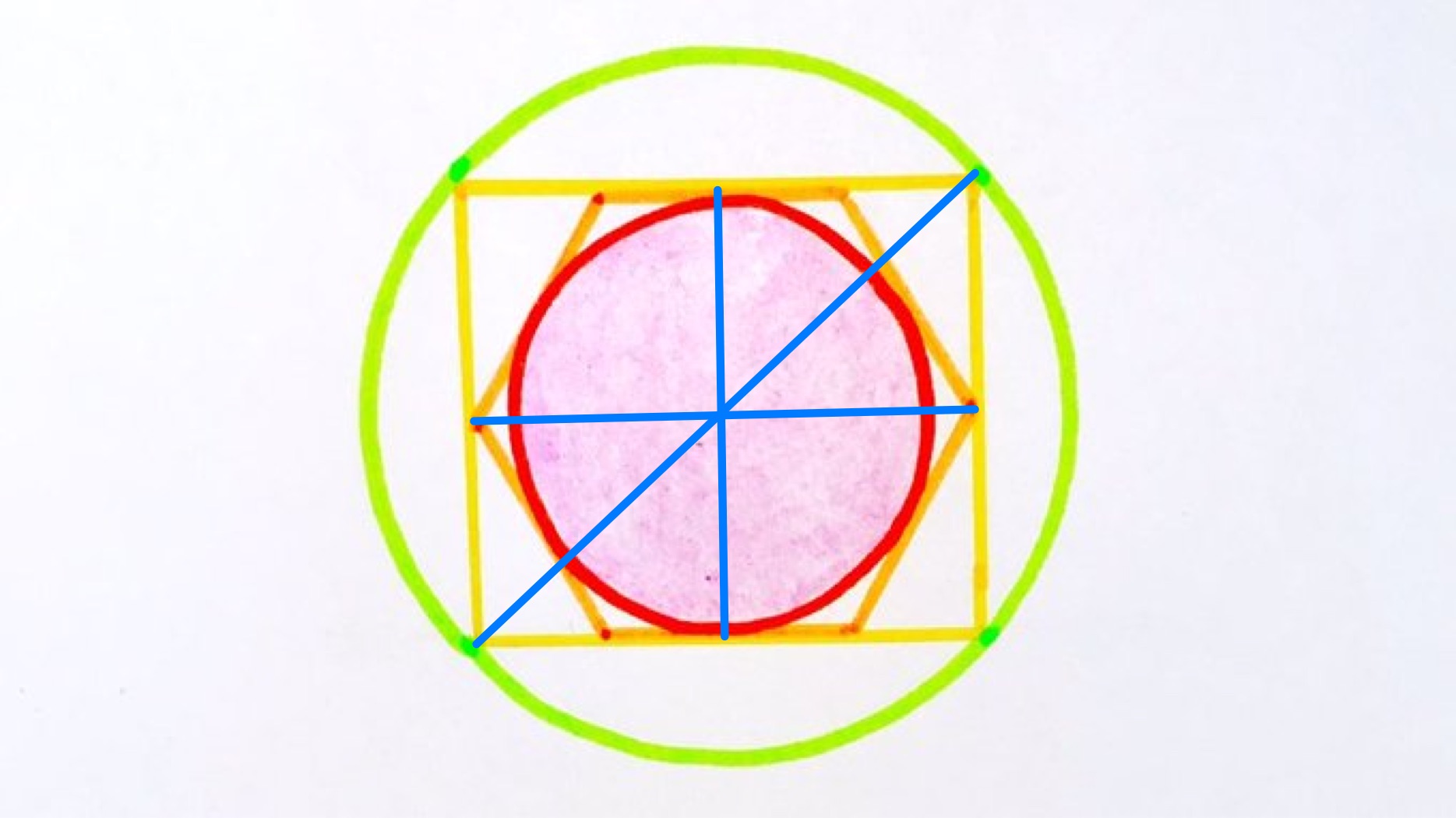
Nested circles and polygons labelled

Let rr be the radius of the inner circle and RR of the outer. The side length of the hexagon is then 23r\frac{2}{\sqrt{3}} r and these lengths are the sides of a right-angled triangle, so by Pythagoras' theorem

R 2=r 2+(23r) 2=r 2+43r 2=73r 2 R^2 = r^2 + \left(\frac{2}{\sqrt{3}} r\right)^2 = r^2 + \frac{4}{3} r^2 = \frac{7}{3} r^2

Therefore the shaded region has area 37\frac{3}{7}ths of the outer circle.

Created on October 2, 2021 18:44:10 by Andrew Stacey
Views: Print | TeX | Source | Linked from: nested circles and polygons