Notes
hexagon in a quarter circle solution
Solution to the Hexagon in a Quarter Circle Puzzle
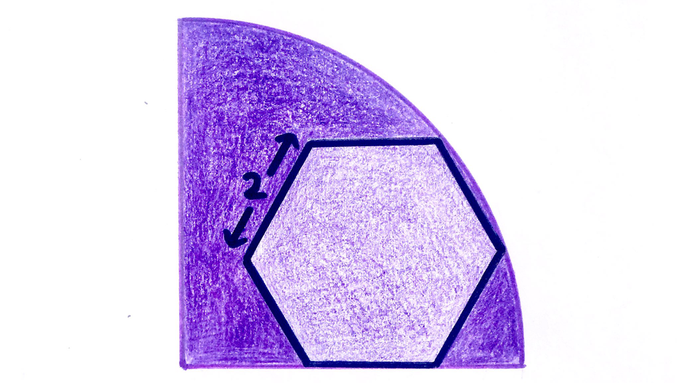
The hexagon is regular. What’s the area of the quarter circle?
Solution by Properties of Chords, Symmetries of Regular Polygons, and Pythagoras' theorem
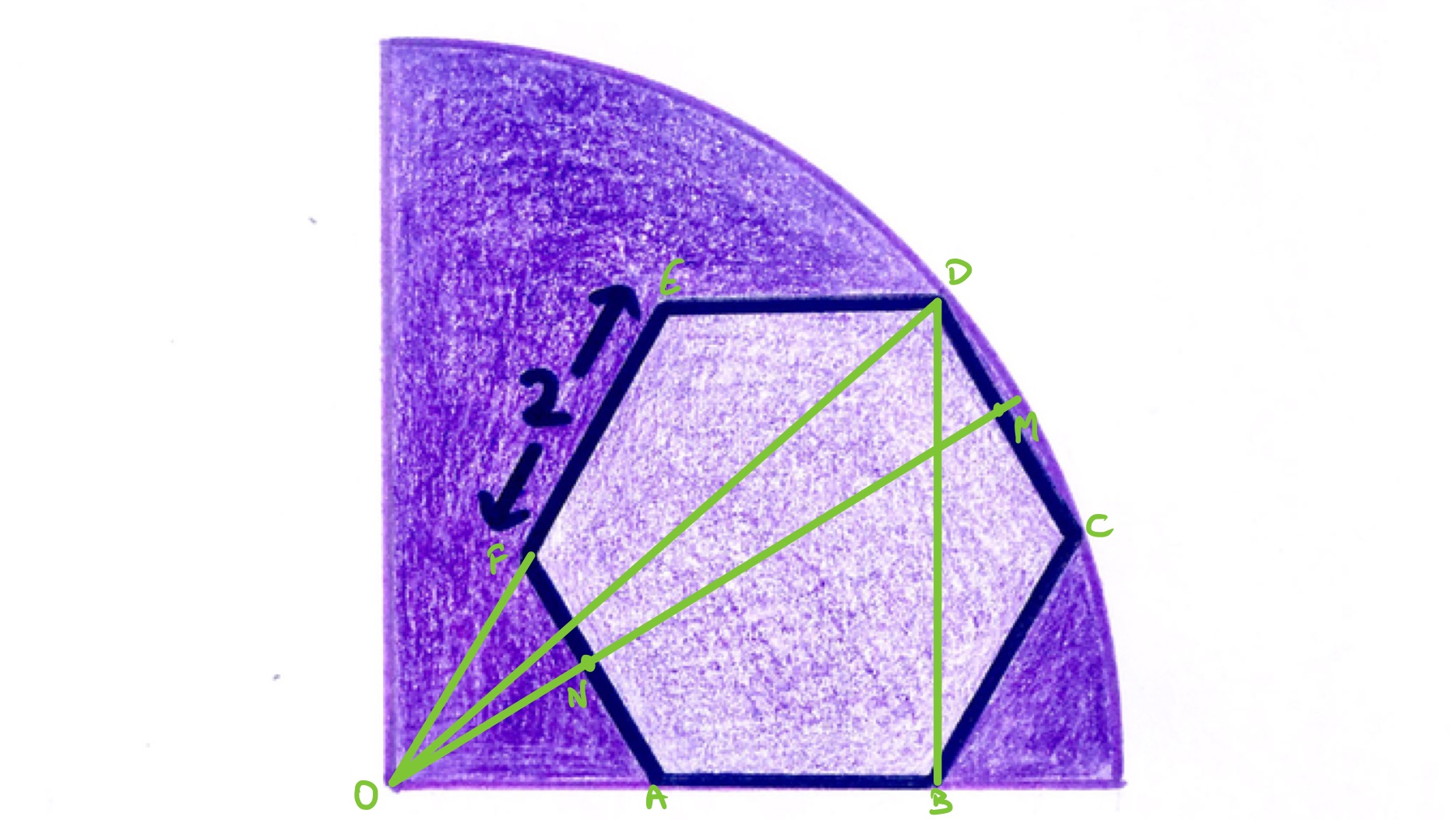
In the above diagram, the line segment is a chord of the quarter circle and so its perpendicular bisector passes through the centre of the circle. It is therefore a line of symmetry of the full circle. It is also a line of symmetry of the hexagon. Reflecting in this line brings to , and to . Since is a straight line, so also must be. Triangle is therefore formed by extending two edges of a regular hexagon and so is an equilateral triangle. In particular, has length and so has length .
The line segment is the height of a regular hexagon which has length times its side length, and so the length of is . Applying Pythagoras' theorem to triangle shows that the square of the length of is . The area of the quarter circle is therefore .