Notes
four squares solution
Solution to the Four Squares Puzzle
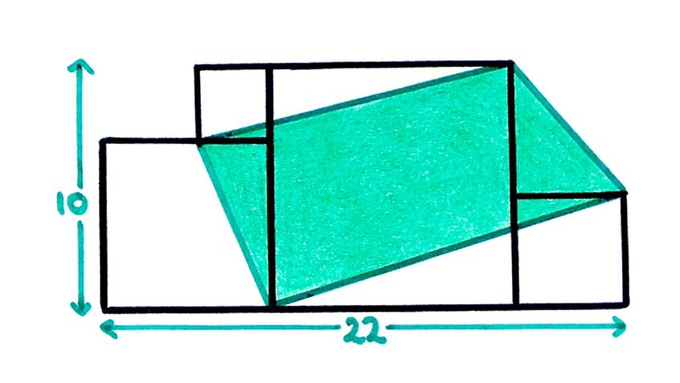
squares. What’s the shaded area?
Solution by Dissection and Calculation
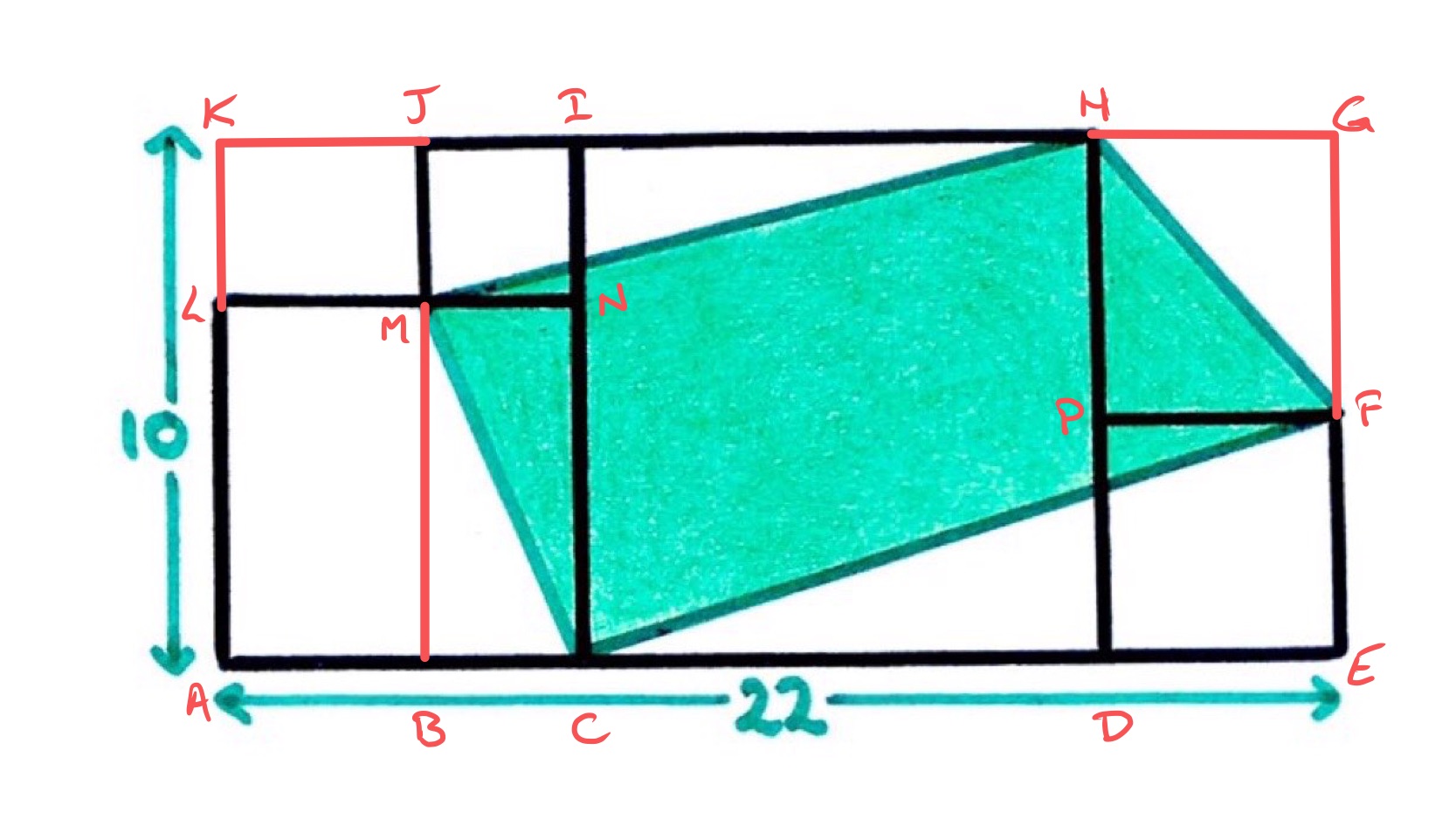
With the points labelled as above, the length of the line segment determines all the other lengths, so let be this length. Then has length , has length , and has length .
The shaded region can be thought of as the rectangle without the four corner triangles. The area of rectangle is , and the areas of the four triangles are as follows.
- Triangle has area
- Triangle has area
- Triangle has area
- Triangle has area
In total, this gives . The shaded area is therefore .
Solution by Shearing and Area of a Triangle
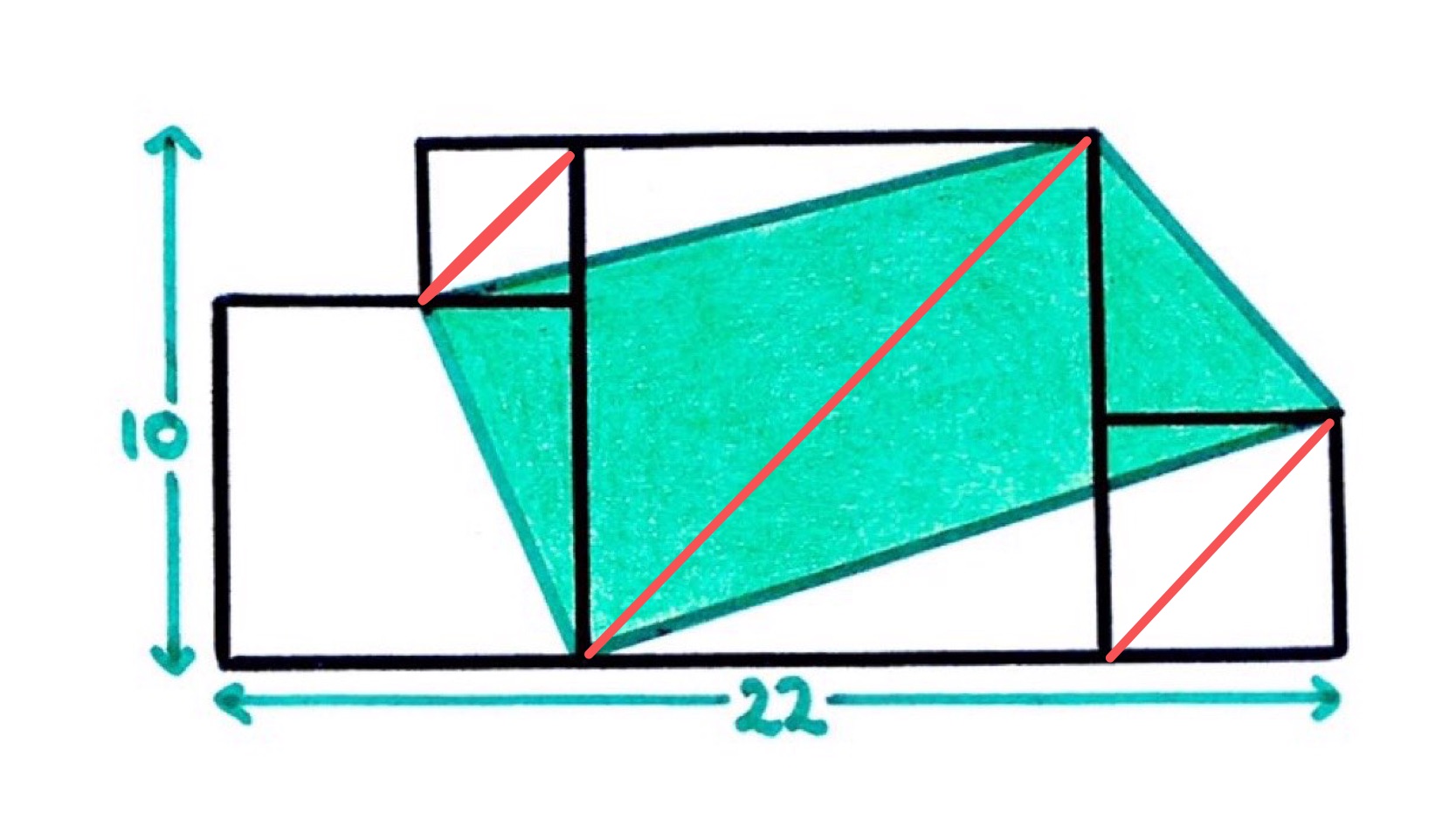
Split the shaded region into two triangles along a diagonal of the central square, as shown above. Each of the outer lines drawn is parallel to this diagonal and so shearing the apex of each triangle along its line does not change its area. Each triangle therefore has area equal to half of the central square, and so the area of the shaded region is the same as that of the central square, which is .
Solution by Invariance Principle
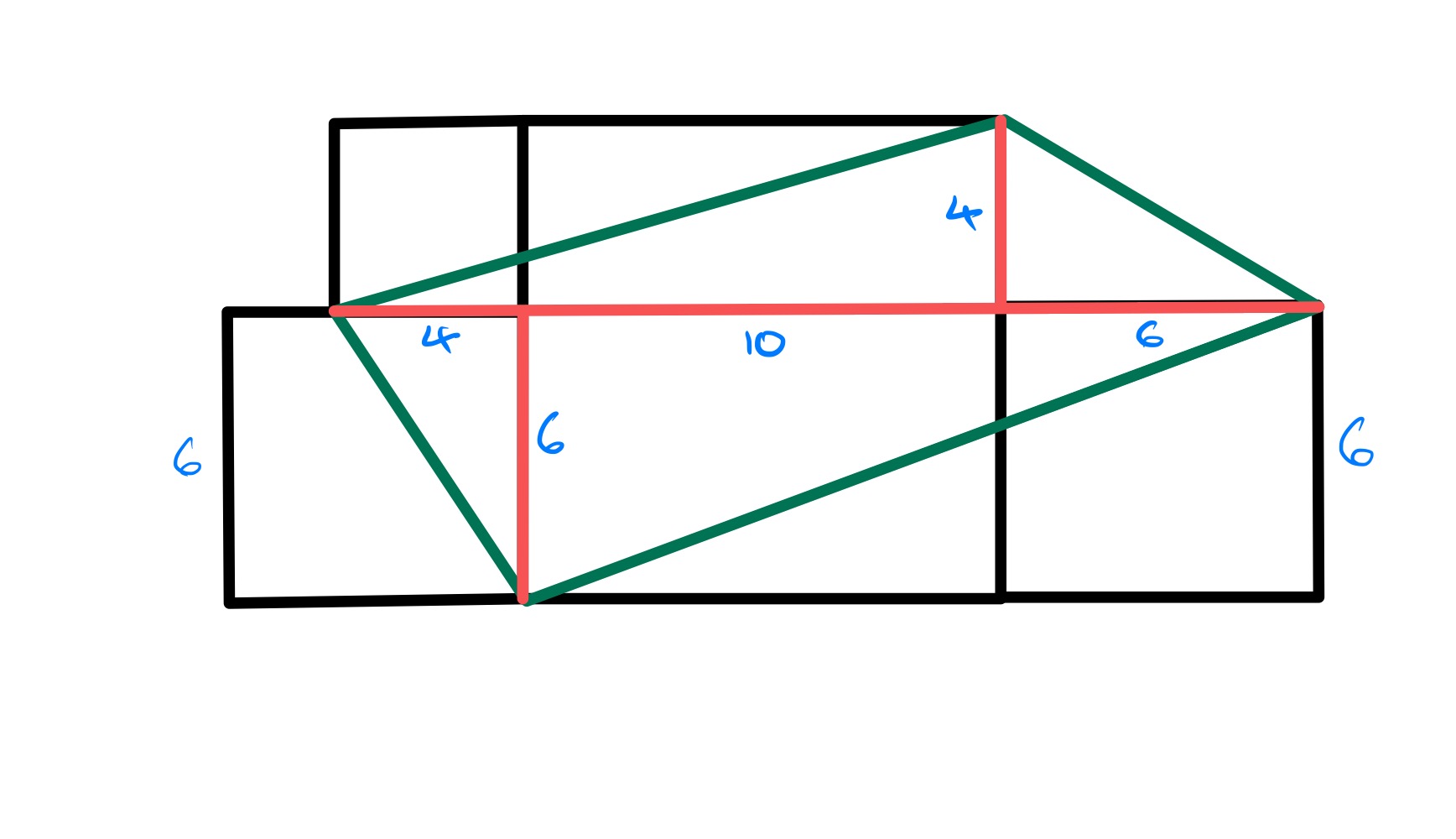
The constraint of the width of the configuration being means that there is not a way to draw this diagram so that the shaded region coincides with the central square. Nevertheless, there is a configuration that allows a simpler calculation, namely when the left and right vertices of the shaded region are level. With the lengths as in the first section, this occurs when , so when . In this configuration, the shaded region can be split into two triangles along a horizontal line from to , which has length . The area of the shaded region is therefore .
Note that this does not show that the area is invariant, but shows that if the area is assumed to be invariant then it must be .