Notes
circle in a hexagon in a semi-circle solution
Solution to the Circle in a Hexagon in a Semi-Circle Puzzle
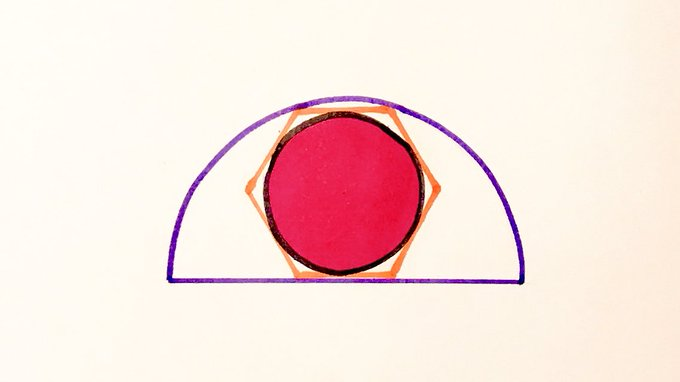
The hexagon is regular. What fraction of the semicircle is shaded?
Solution by Lengths in a Regular Hexagon and Pythagoras' Theorem
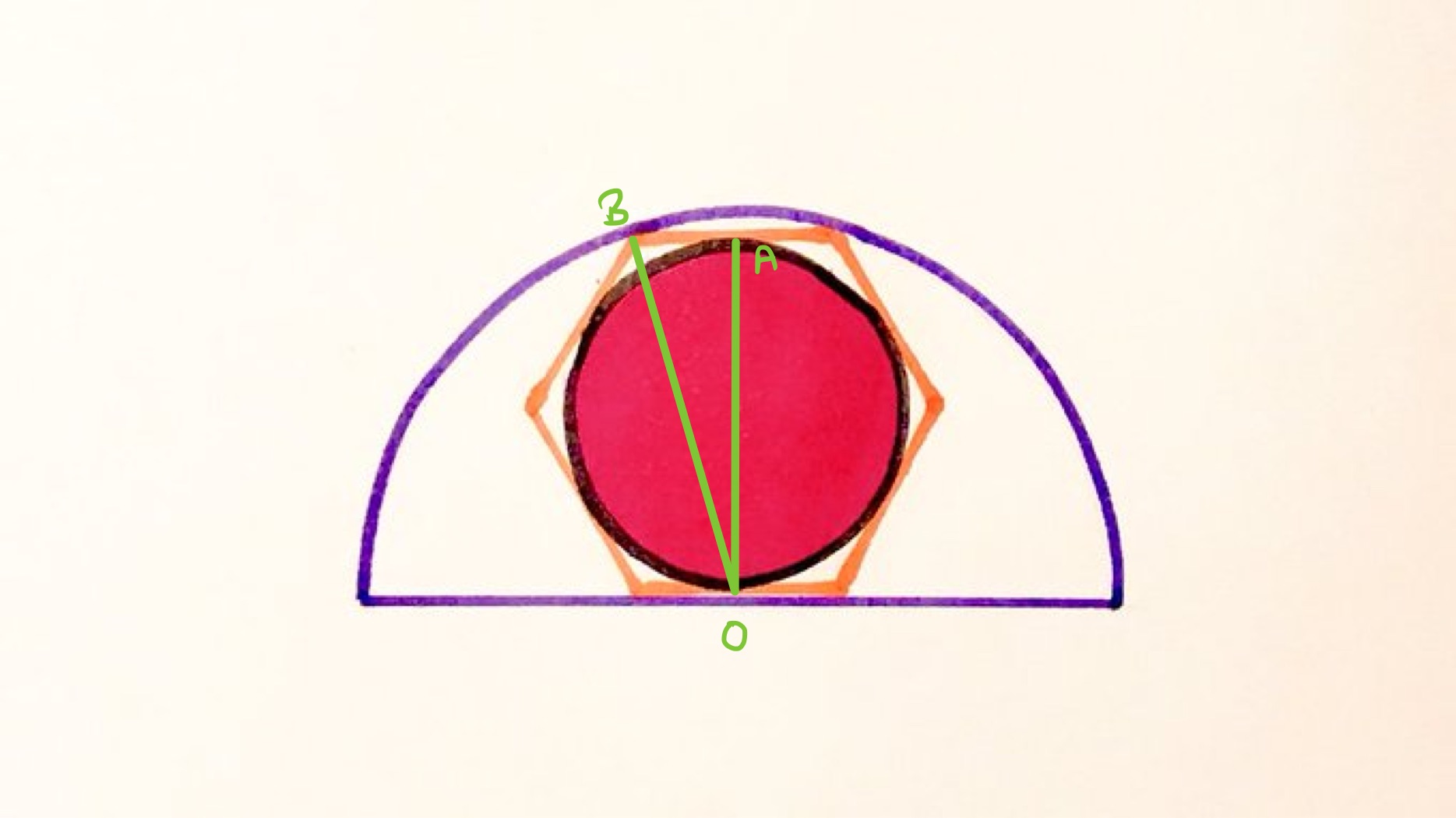
In the above diagram, the point is the centre of the circle and the point is the midpoint of the top edge of the hexagon. As that top edge is a chord of the circle, its perpendicular bisector passes through the centre so is also the midpoint of the bottom edge.
Let be the radius of the shaded circle and the radius of the semi-circle, so has length and has length . By considering the lengths in a regular hexagon, the length of is times the side length of the hexagon, so has length . Applying Pythagoras' theorem to triangle shows that:
Since the area of the circle is and of the semi-circle is , the fraction of the semi-circle that is shaded is .