Notes
arcs in a circle solution
Solution to the Arcs in a Circle Puzzle
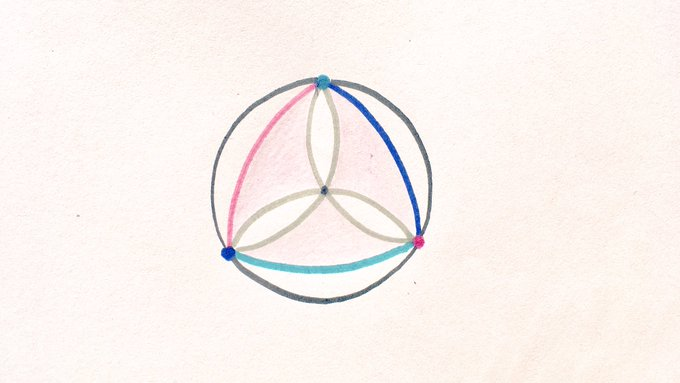
What fraction is shaded? Three coloured dots are equally spaced around the circle, with an arc (of the same colour) centred on each dot. The other arcs intersect at the centre of the circle.
Solution by Sectors of a Circle and Lengths in an Equilateral Triangle
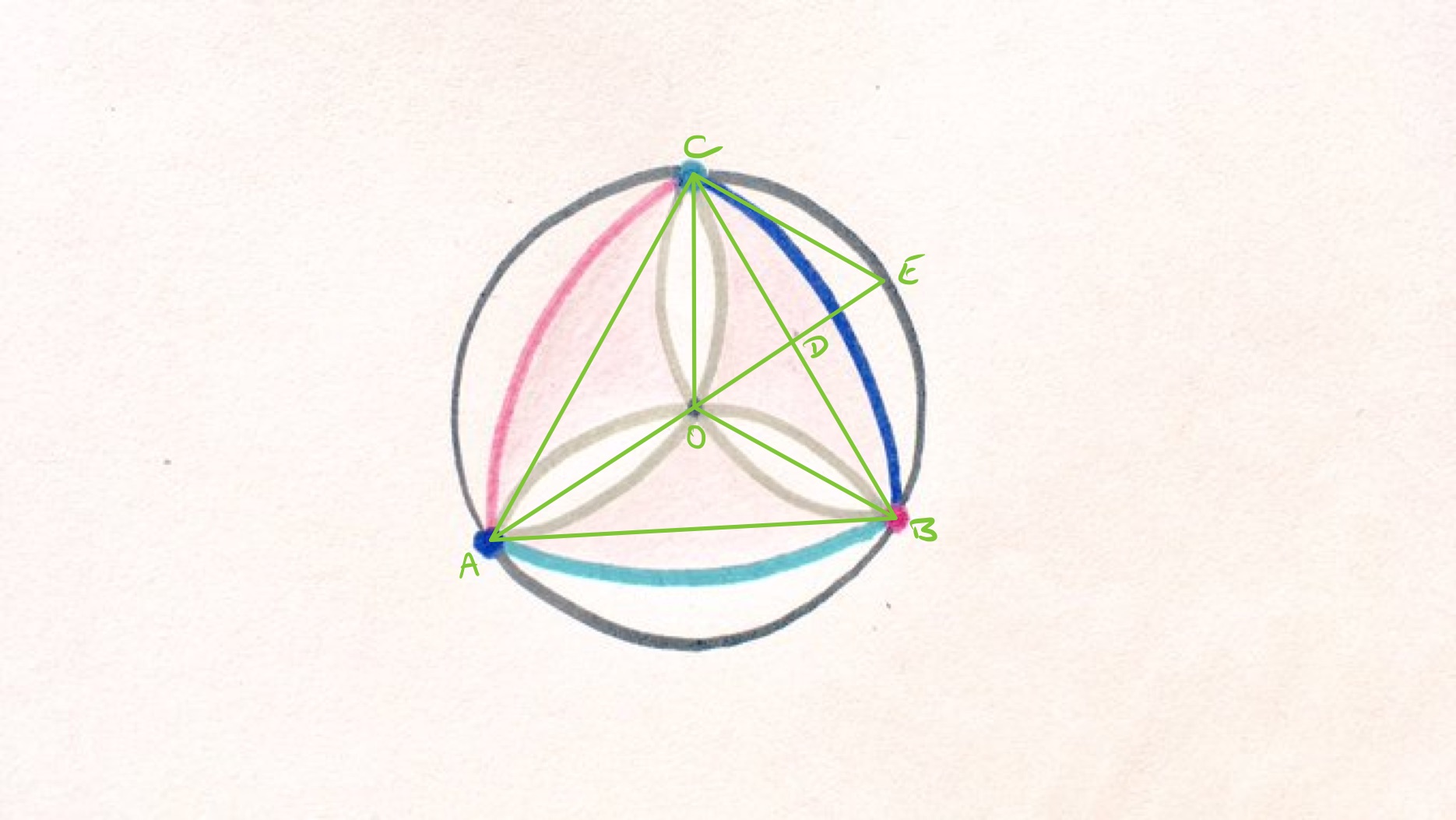
With the points labelled as above, consider the region bounded by the line segments , , and the arc . As the points are equally spaced around the circle, triangle is an equilateral triangle so angle is and so the region is a sector of a circle with radius and central angle . Its area is therefore one sixth of that of a circle with radius .
Now consider the shaded region bounded by the arcs , , and . This is part of the sector considered above. To determine the area of the difference, consider the region bounded by the line segments , , and the arc (curved to the left of the diagram). Since triangle is congruent to triangle , this region has the same area as that bounded by line segments and and arc . This is a sector of a circle with radius and central angle .
From lengths in an equilateral triangle, triangle has area three times of that of triangle . Therefore, the circle of radius has area three times that of the circle of radius . Let us write for the area of the outer circle. Then the shaded area bounded by the arcs , , and has area:
As the full shaded area comprises three such regions, its area is . The shaded area is thus half of the area of the full circle.