Notes
a circle and two semi-circles in two hexagons solution
Solution to the Circle and Two Semi-Circles in Two Hexagons Puzzle
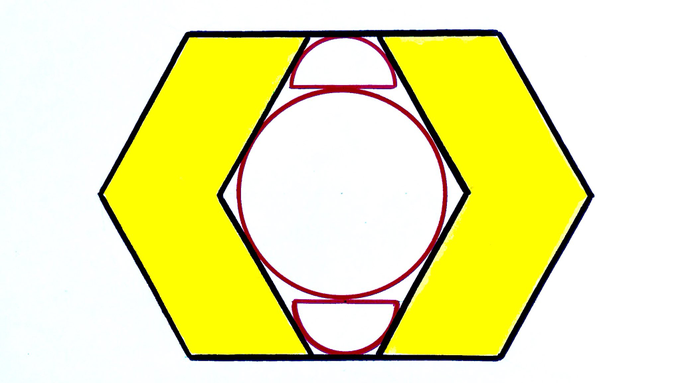
A circle and two semicircles are trapped by two overlapping regular hexagons. What fraction of the total area is shaded?
Solution by Angles in an Equilateral Triangle and Regular Hexagon
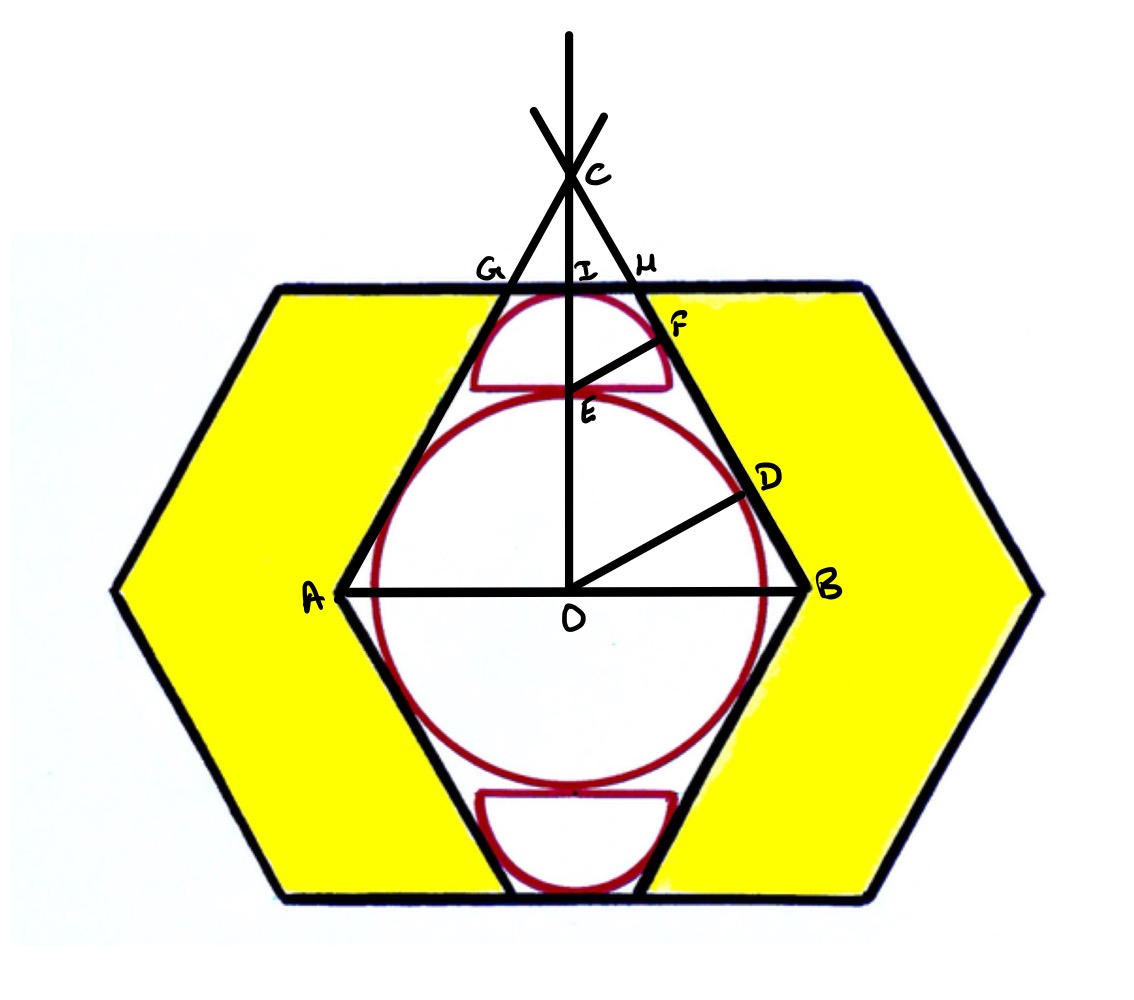
In the above diagram, the edges and are extended to meet at . The point is the centre of the larger circle and of the upper semi-circle.
Angles and are both so triangle is an equilateral triangle. Angle is a right-angle as it is the angle between a radius and tangent and angle is half of , so triangle is half an equilateral triangle, so the length of is half that of . Hence the length of is the same as that of . A similar argument applies to the triangle so the length of is the same as that of . Putting that together shows that the length of is a third of that of . So the length of is a third of the length of , which is a side of one of the hexagons.
This means that dividing each side of the hexagon in three and drawing lines parallel to the sides is a subdivision of each of the regions.
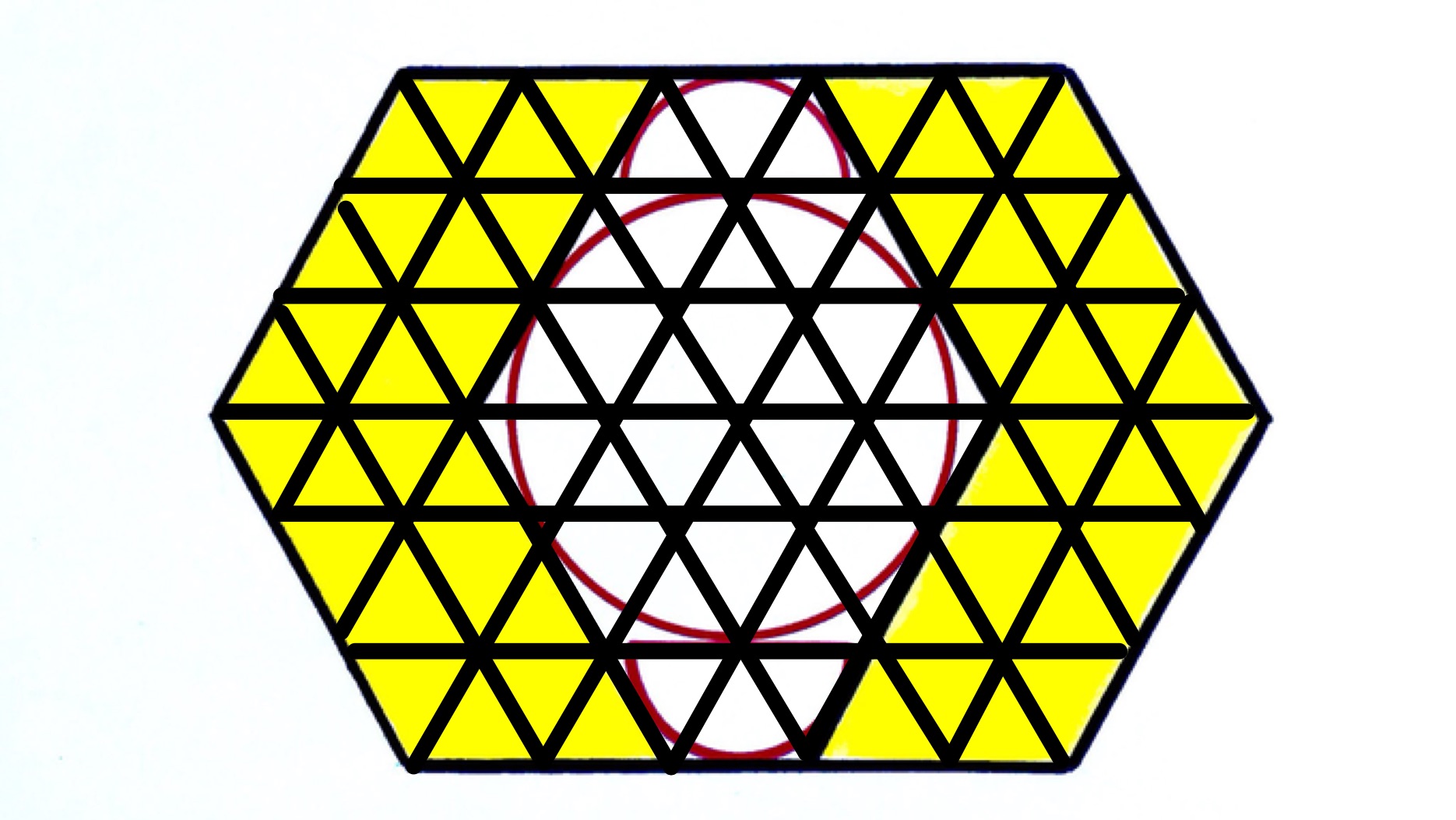
There are triangles in each of the yellow regions, and in the white region. So there are in total and that are yellow, so the yellow region is ths of the total.