Notes
zig-zag inside a square solution

Solution to the Zig-zag Inside a Square Puzzle

Solution by Area of a Triangle and Similar Triangles

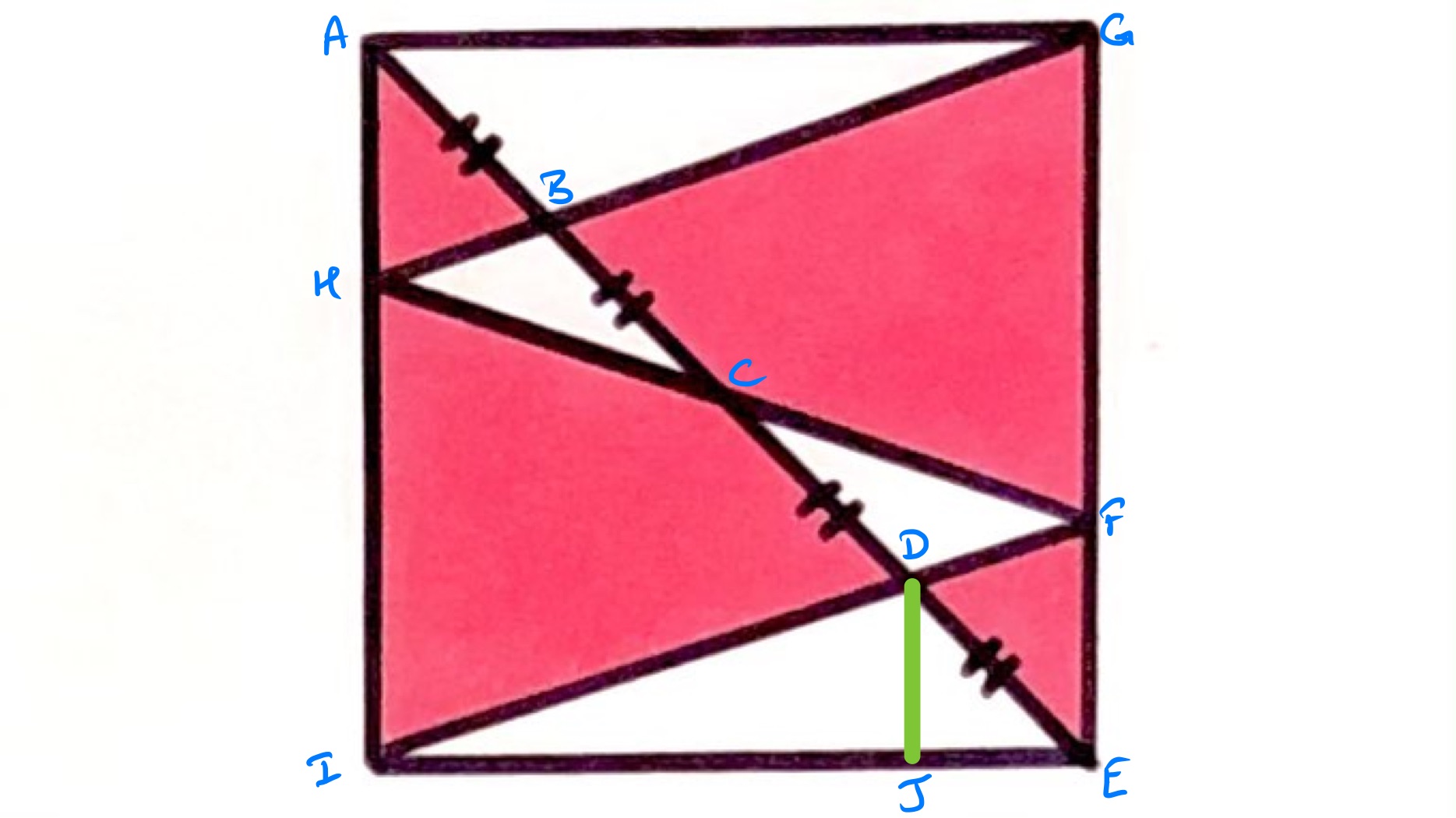
The first observation is that the smaller triangles are equal in area. Specifically, with the points labelled as above, then triangles $D E F$ and $C D F$ have the same area. This can be seen by taking $D E$ and $C D$ as the bases with $F$ as the highest point of both. From the problem, $D E$ and $C D$ have the same length, and then obviously they have the same height above this base. This means that the white area has the same area as of the triangles $I E F$ and $G A H$. Putting these rectangles together creates a rectangle whose width is the same as the side of the outer square and whose height is $F E$, so the key to the problem is finding the length of $F E$.

The triangle $A E F$ is similar to the triangle $I J D$. As $D$ is one quarter of the way from $E$ to $A$, the height of $D$ above $J$ is one quarter of the side length of the outer square. It is also one quarter of the way across from $E$, meaning that $J$ is three quarters of the way from $I$. So $I J$ is three times longer than $J D$. As this ratio is preserved by similar triangles, the segment $I E$ is three times longer than $F E$. This means that $F E$ is one third of the height of the square.

The white area is therefore one third of the square, and so the shaded area is two thirds of the square.