Notes
zig-zag inside a rectangle solution
Solution to the Zig-zag Inside a Rectangle Puzzle
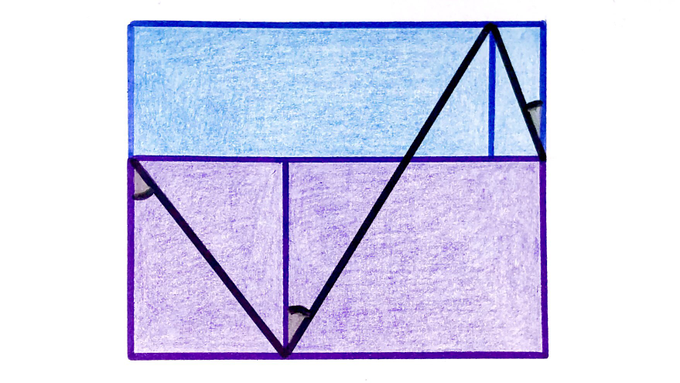
Rectangles of the same colour are similar. What’s the sum of the three marked angles?
Solution by Similar Triangles, Angles in a Triangle, Angles in a Semi-Circle, and Angles in the Same Segment
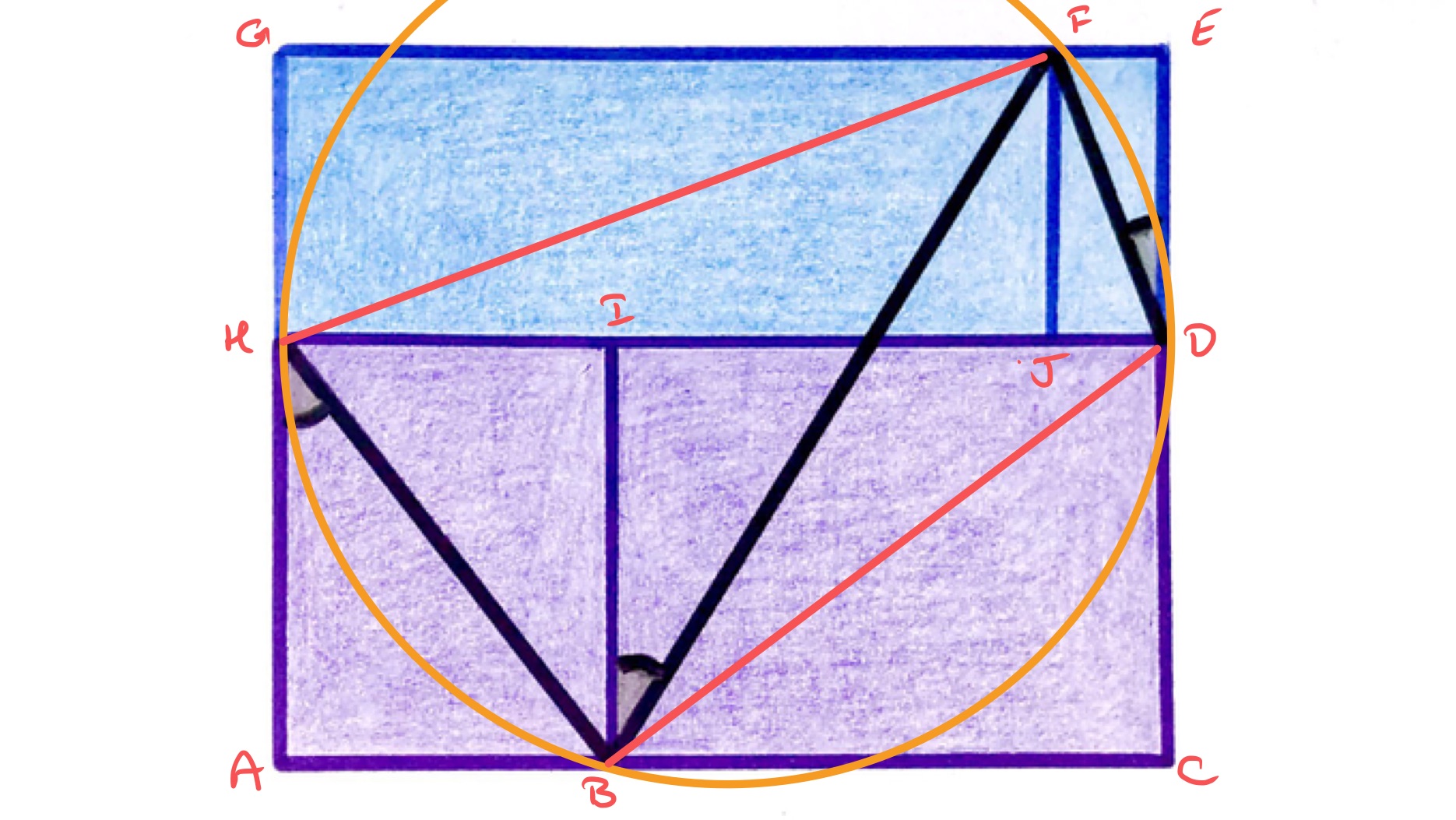
In the above diagram, the orange circle is drawn so that is a diameter.
The purple rectangles are similar, so triangles and are also similar, with the vertices corresponding in that order. So angles and are the same. Since angle is a right-angle, this means that angles and add up to , so angle is a right-angle. Since the angle in a semi-circle is a right-angle, this means that lies on the orange circle.
By a similar argument, so also lies on the orange circle.
As the blue rectangles are similar, angles and are the same. Since angles in the same segment are equal, the angle is also the same as and as . Lastly, triangles and are congruent so angles and are equal, so the three marked angles add up to angle which is .