Notes
upside-down semi-circles in a semi-circle solution
Solution to the Upside-Down Semi-Circles in a Semi-Circle Puzzle
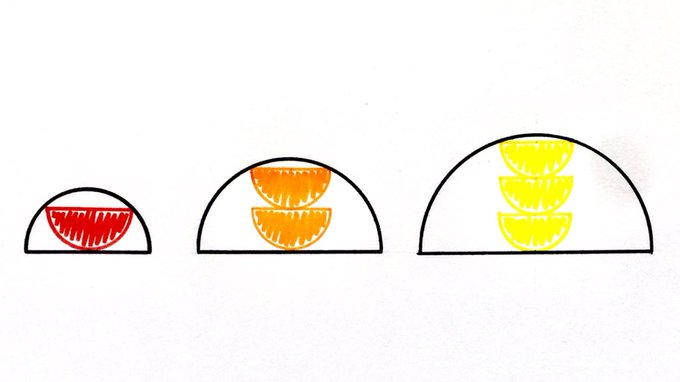
What proportion of each diagram is shaded? Give your answers as decimals. What comes next?
Solution by Pythagoras' Theorem
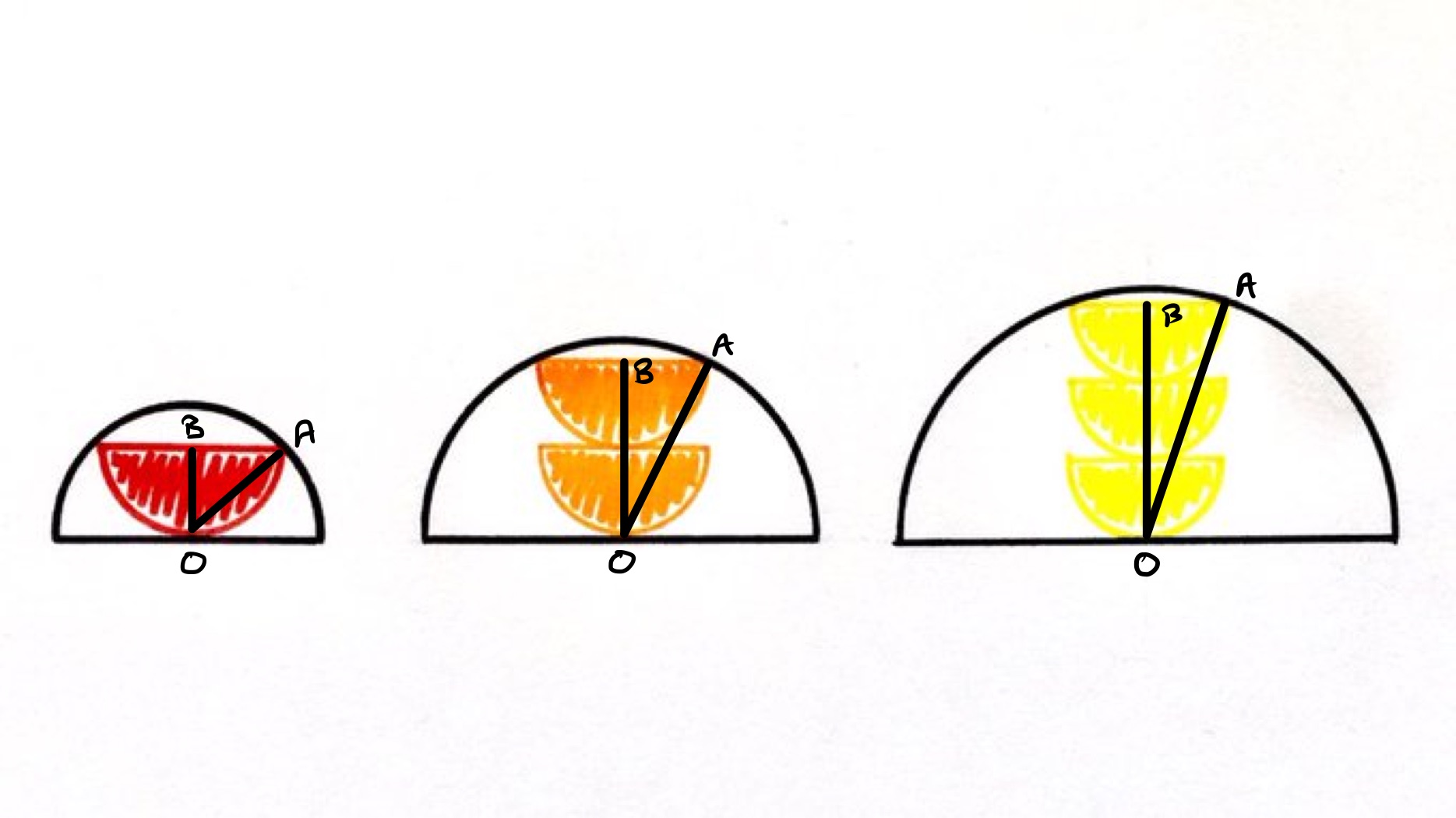
Fix a diagram with small semi-circles. Let be the radius of the small semi-circles and of the outer one. In that diagram, triangle is right-angled. The length of is while the length of is . Applying Pythagoras' theorem shows that:
The shaded area is while the area of the outer semi-circle is . The proportion that is shaded is therefore . The first few values of this are: