Notes
two triangles overlapping a rectangle solution
Solution to the Two Triangles Overlapping a Rectangle Puzzle
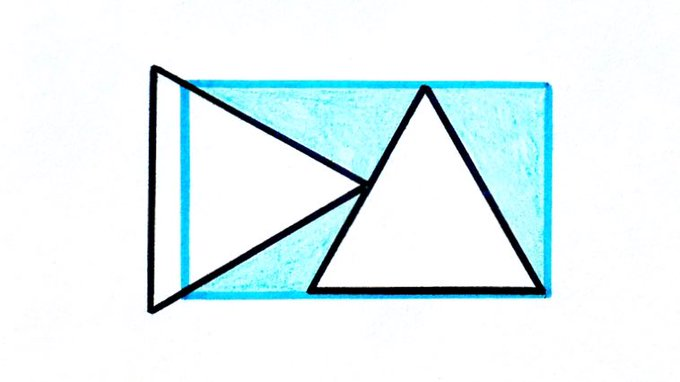
What fraction of the rectangle is not covered by these two equilateral triangles?
Solution by Lengths in an Equilateral Triangle
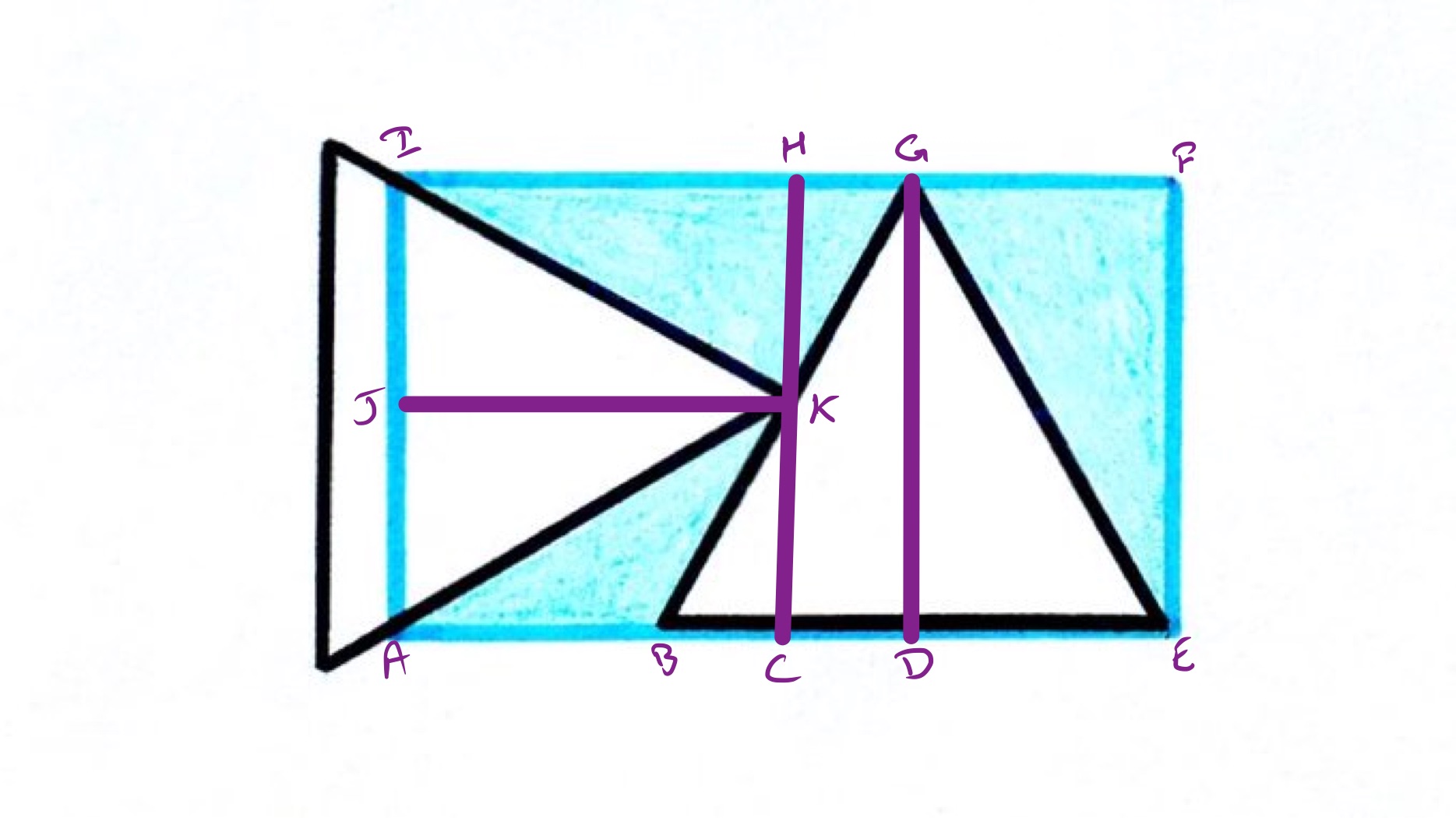
Let be the side length of the right-hand triangle, so the length of . From lengths in an equilateral triangle, the length of is . As this is the length of , the length of is times this, so is .
Since is horizontally aligned with which is the midpoint of , it is also the midpoint of and so is the midpoint of . Therefore, is and so the width of the rectangle is .
The blue regions can be matched with the white (inside the rectangle) except for the strip between and : triangle matches , triangle matches , the combination of triangle with matches . Therefore the blue regions comprise half of the rectangle without the strip between and . This strip has width , meaning that the rest of the rectangle (which is split between the white and blue regions) is equivalent to a rectangle with width (and the same height as the main rectangle). Half of this is blue, so the blue regions are equivalent to a rectangle of width . Therefore the blue regions form ths of the rectangle.