Notes
two triangles in a semi-circle solution

Solution to the Two Triangles in a Semi-Circle Puzzle

Solution by Perpendicular Bisector of a Chord, Properties of Isosceles Triangles, and Congruent Triangles

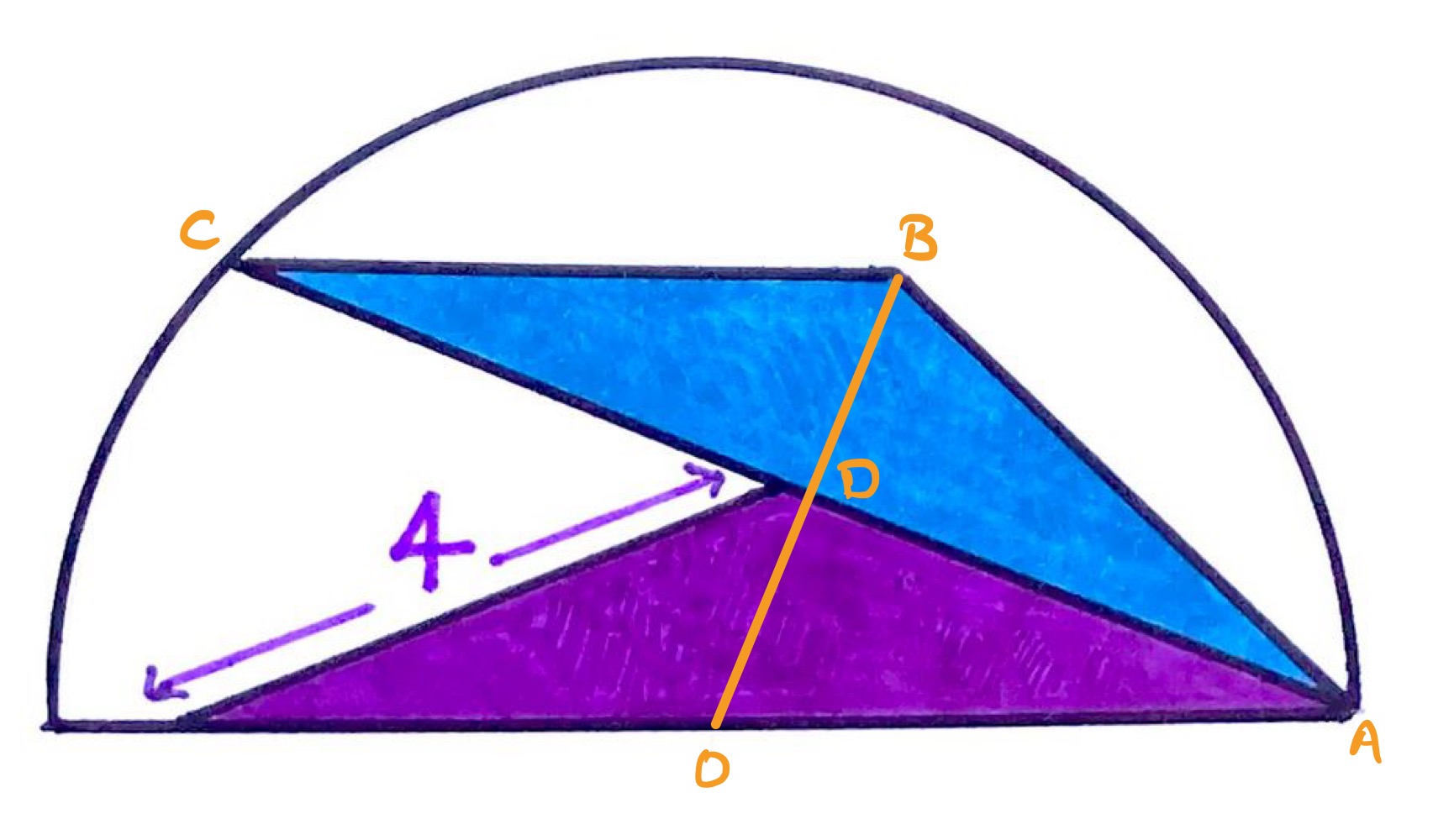
In the diagram above, $O$ is the centre of the semi-circle and $D$ is the midpoint of chord $A C$. As such, the perpendicular bisector of $A C$, which passes through $D$, also passes through $O$.

Since $A C$ is the base of the isosceles triangle $A B C$, that perpendicular bisector also passes through $B$. So $B D O$ is a straight line.

Triangles $B D A$ and $O D A$ are both right-angled at $D$. Since the blue and purple triangles are congruent, angles $B \hat{A} D$ and $D \hat{A} O$ are equal. Therefore, triangles $A D B$ and $A D O$ have the same interior angles and share side $A D$ so are congruent.

This means that line segments $A B$ and $A O$ have the same length. Then since the triangles are congruent and isosceles, $A B$ has length $4$, so the radius of the semi-circle is also $4$ and its area is then: