Notes
two triangles in a rectangle solution
Solution to the Two Triangles in a Rectangle Puzzle
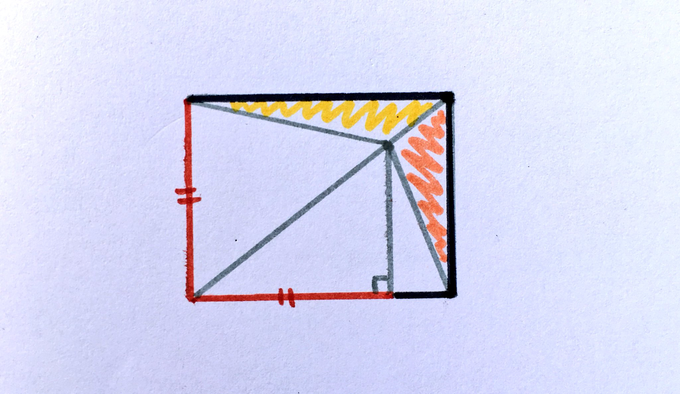
Show that the two shaded areas cover the same proportion of the rectangle.
Solution by Similar Triangles and Area of a Triangle
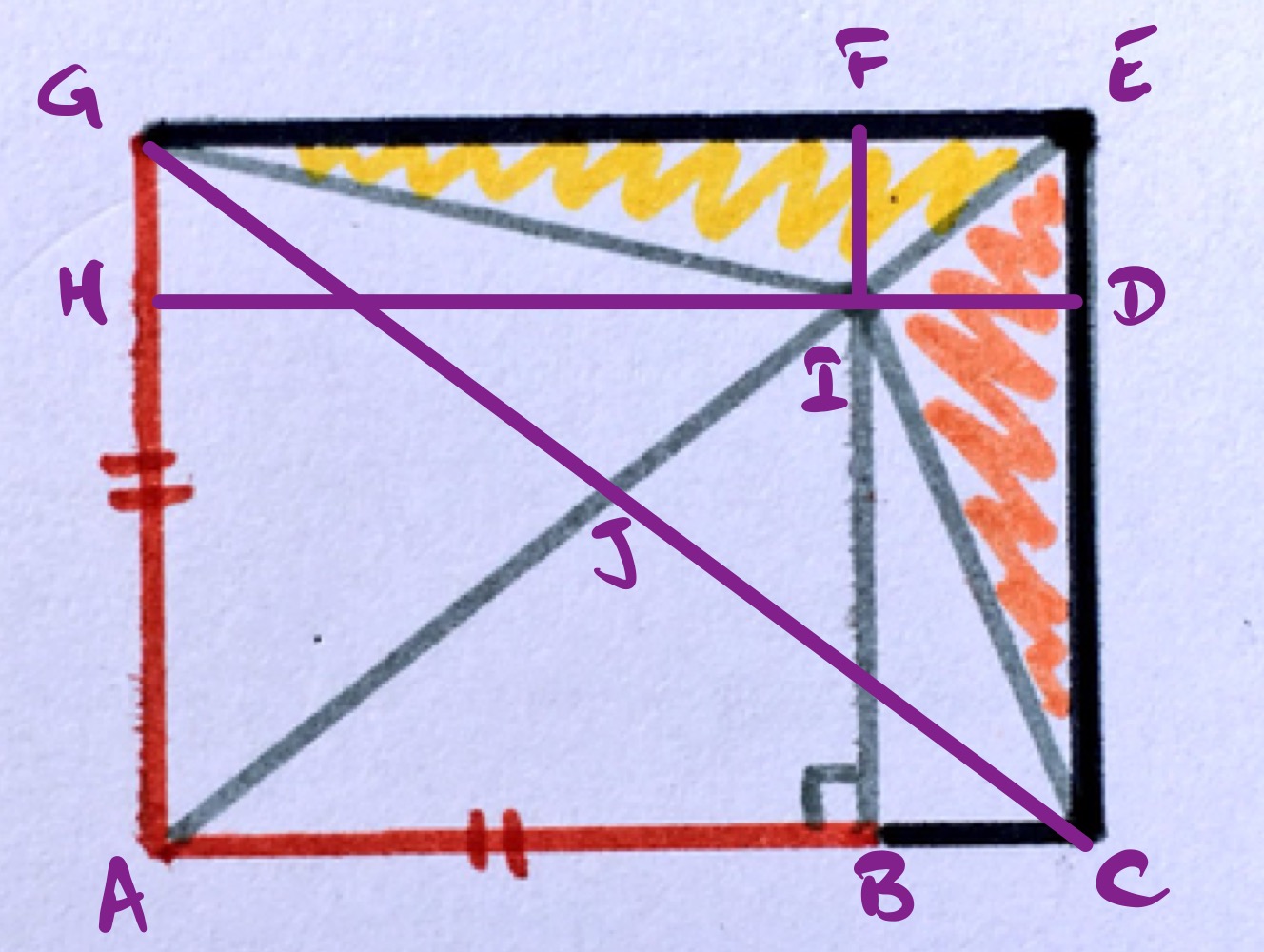
With the diagram labelled as above, let and be the lengths of the sides of the outer rectangle, with the length of and the length of .
Then has length , so the area of the orange triangle, , is .
Let be the length of , so has length . The area of the yellow triangle is then .
Triangle is similar to triangle since both share angle and both are right-angled triangles. Therefore, which rearranges to . This means that .
Hence the area of the yellow triangle is which is the area of the orange triangle.
Solution by Area of a Triangle
With the same diagram as above, consider the triangles and . To work out their areas, we need the perpendicular height of above and the lengths of and . Since is the midpoint of , these lengths will be the same and so the areas of and are the same.
Then triangles and also have the same area since each is a quarter of the full rectangle. Therefore, the orange and yellow areas are the same.
(A similar result follows by considering triangles and and noting that the perpendicular height of above is the same as that of .)