Notes
two triangles and three concentric semi-circles solution
Solution to the Two Triangles and Three Concentric Semi-Circles Puzzle
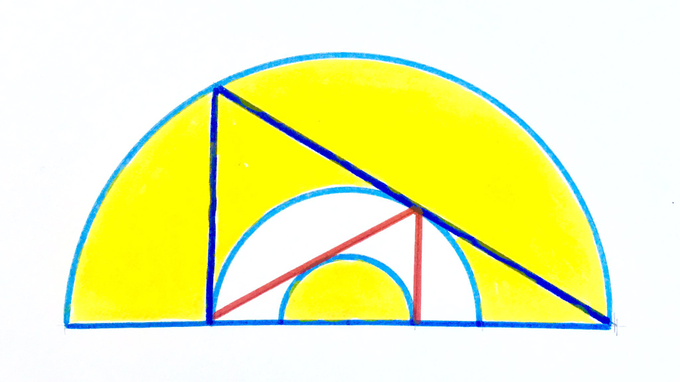
Two right-angled triangles and three concentric semicircles. What fraction is yellow?
Solution by Similar Triangles
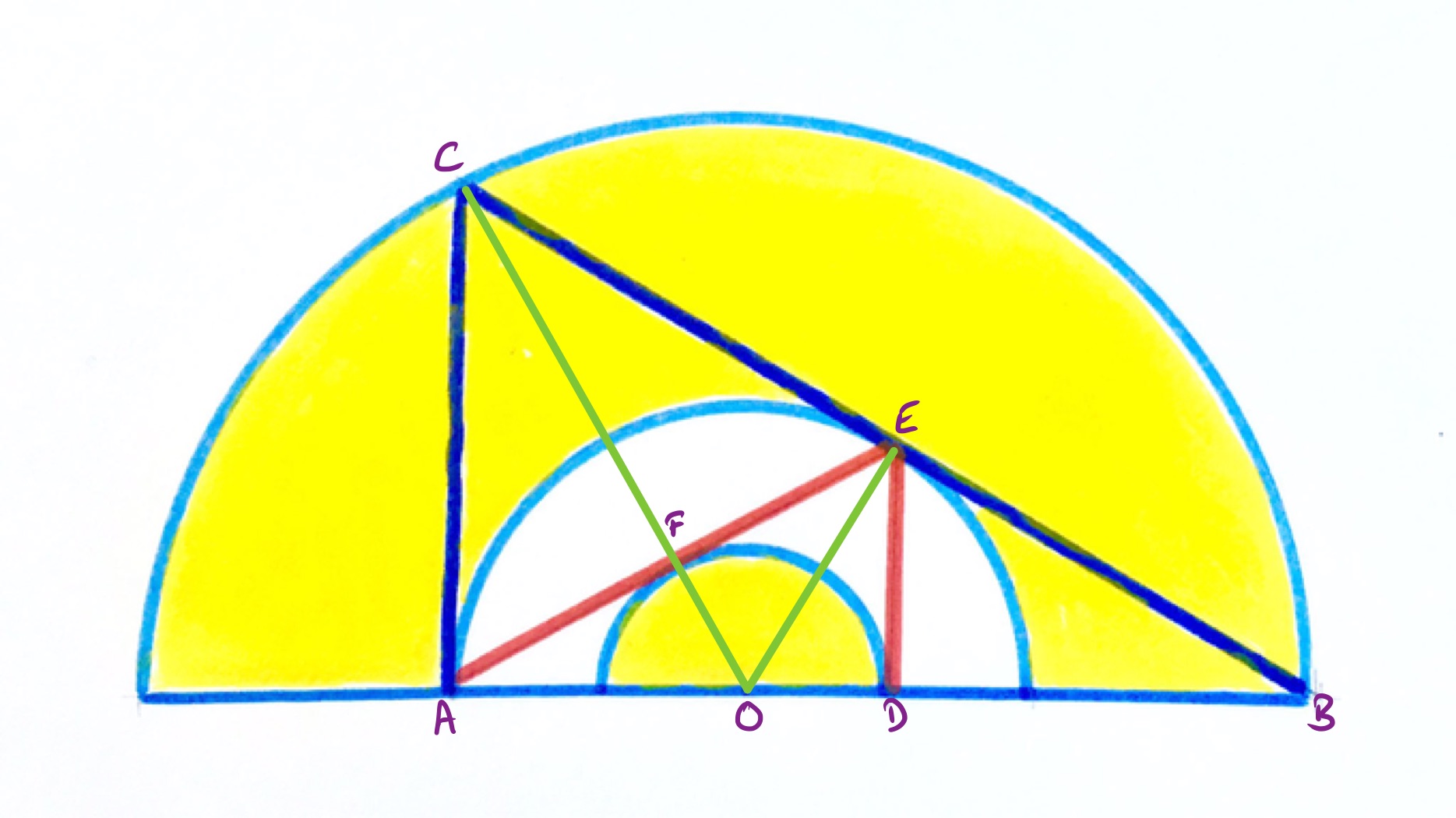
In the above diagram, point is the centre of the concentric semi-circles.
Consider the smaller triangle and the two smaller circles. Point is where the side touches the circle, so angle is a right-angle as it is the angle between a radius and tangent. Triangles , , and are all right-angled triangles with and of the same length, and and of the same length. They are therefore congruent. They are also similar to triangle as triangles and are both right-angled triangles sharing the angle at . The congruency shows that the length of is twice that of , and so by similarity has double the length of . Therefore the middle semi-circle has double the radius of the smaller one.
Applying the same argument to the triangle shows that the outer semi-circle has double the radius of the middle semi-circle, and so four times that of the smaller semi-circle.
Since area scales with the square of the length scale factor, the area of the outer semi-circle is times that of the smallest, while the middle semi-circle has area times that of the smallest. The white region therefore has area times that of the smallest and so the fraction that is shaded is .
Solution by Equilateral Triangles
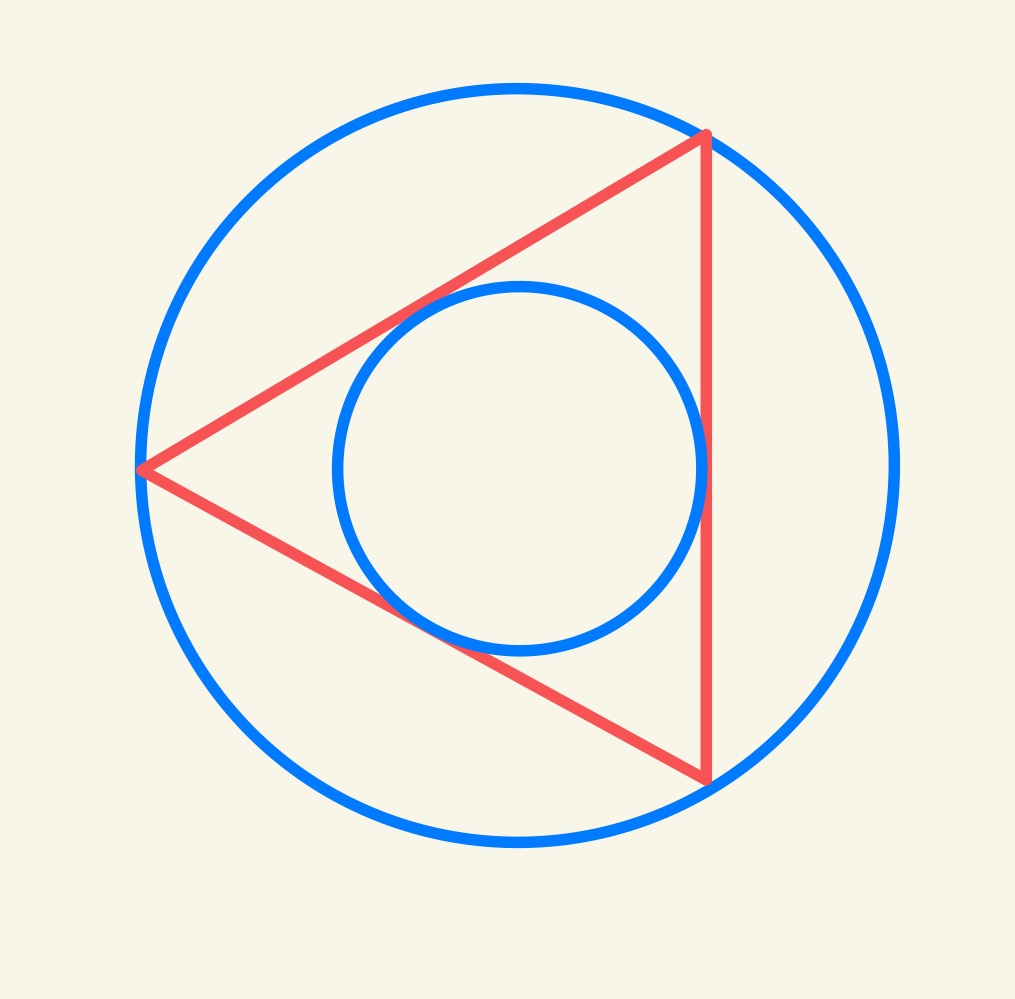
Reflecting the diagram to create whole circles shows that the original triangles are half of a triangle with the property that its circumcircle and in-circle are concentric. Such a triangle must be equilateral, and the radius of its circumcircle is double that of its in-circle. The result then follows as above.