Notes
two tilted squares solution
Solution to the Two Tilted Squares Puzzle
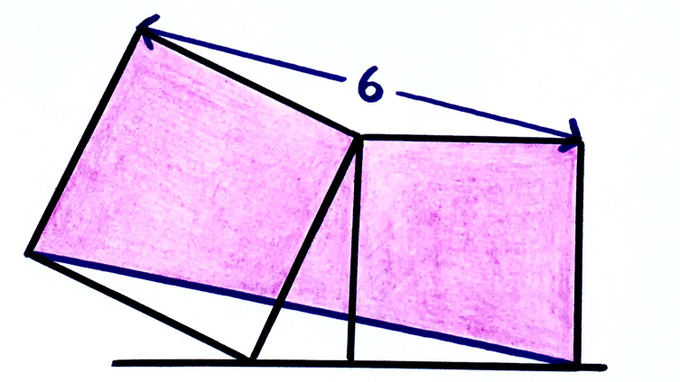
Two squares. What’s the total pink area?
Solution by Pythagoras' Theorem and Congruent Triangles
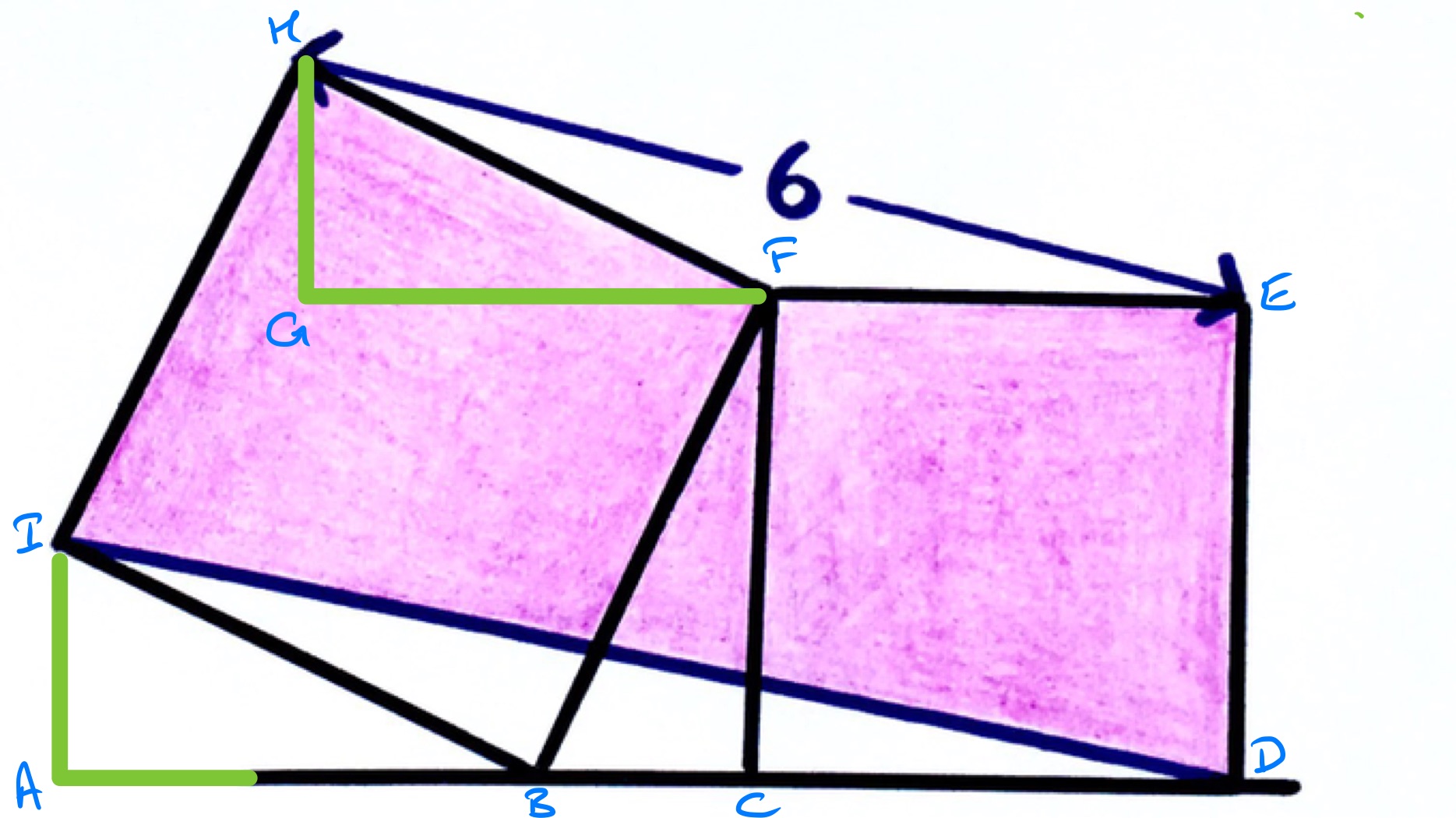
With the points labelled as in the above diagram, let , , and be the lengths of sides , , and respectively. Applying Pythagoras' theorem to triangle results in .
Triangles , , and are all right-angled triangles with hypotenuse a side of the square and angle , , and are all equal, so the triangles are all congruent.
Since and are of length , applying Pythagoras' theorem to triangle results in .
The area of the pink region can be found by finding the area of the full region and subtracting the area of the bottom triangle, . The squares have areas and , the middle triangle has area . Triangle has base of length and height of length . So it has area . The area of the pink region is therefore:
Solution by Invariance Principle
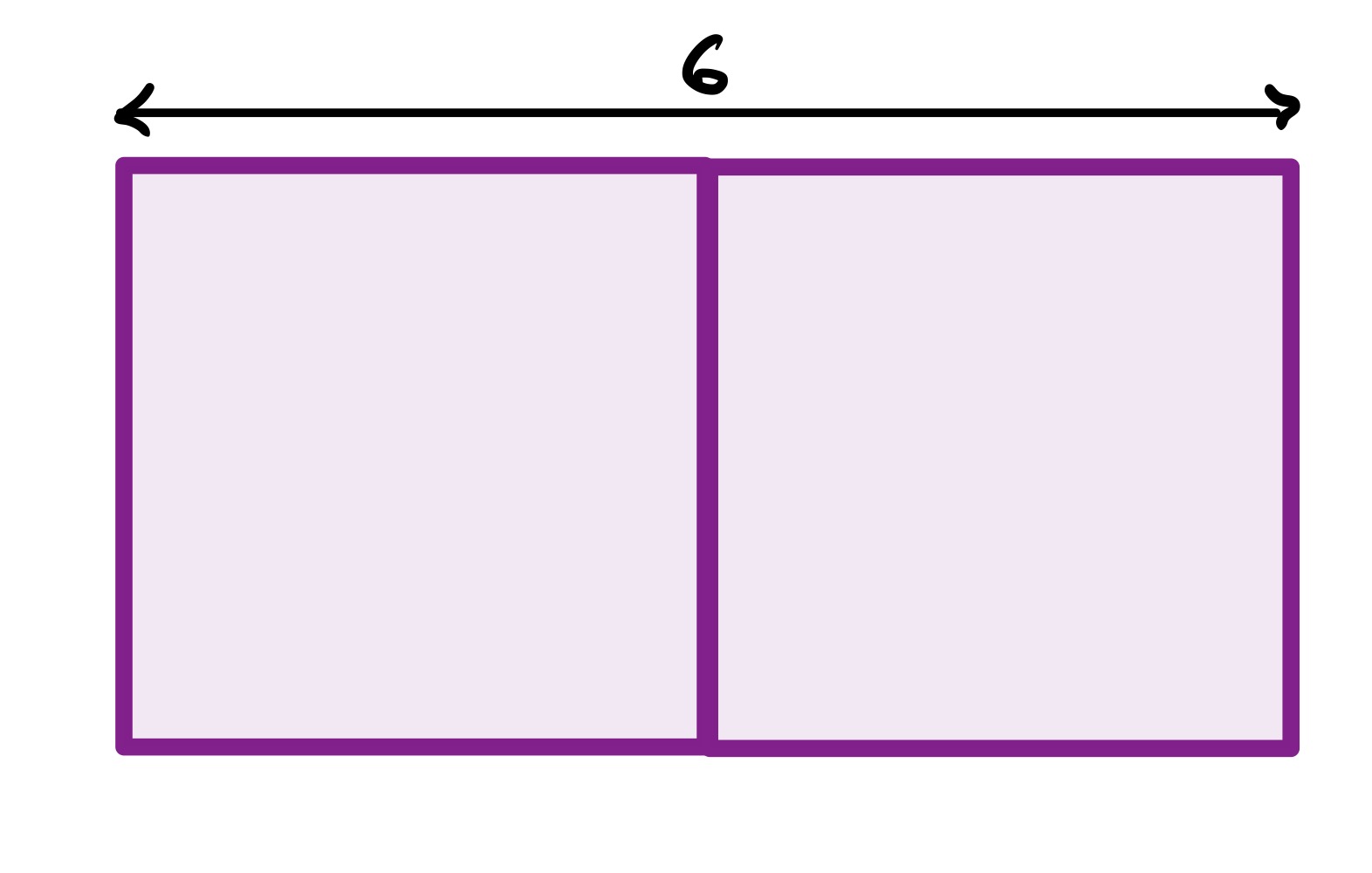
In this version of the diagram, the two squares are aligned and so the total distance across both is meaning that each has a side length of . Their area is then .