Notes
two squares solution
Two Squares
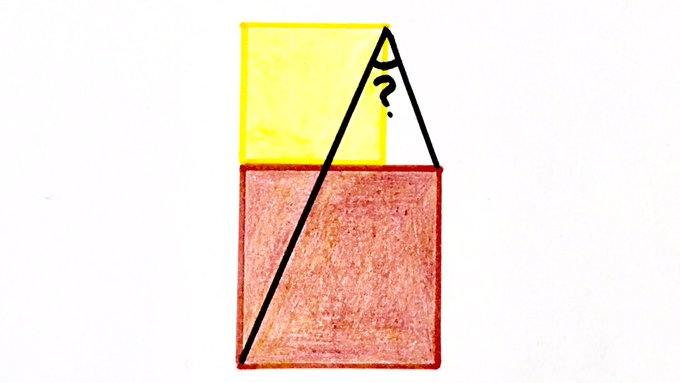
The red square has double the area of the yellow square. What’s the angle?
Solution by Properties of Squares and Angle at the Circumference is Half the Angle at the Centre
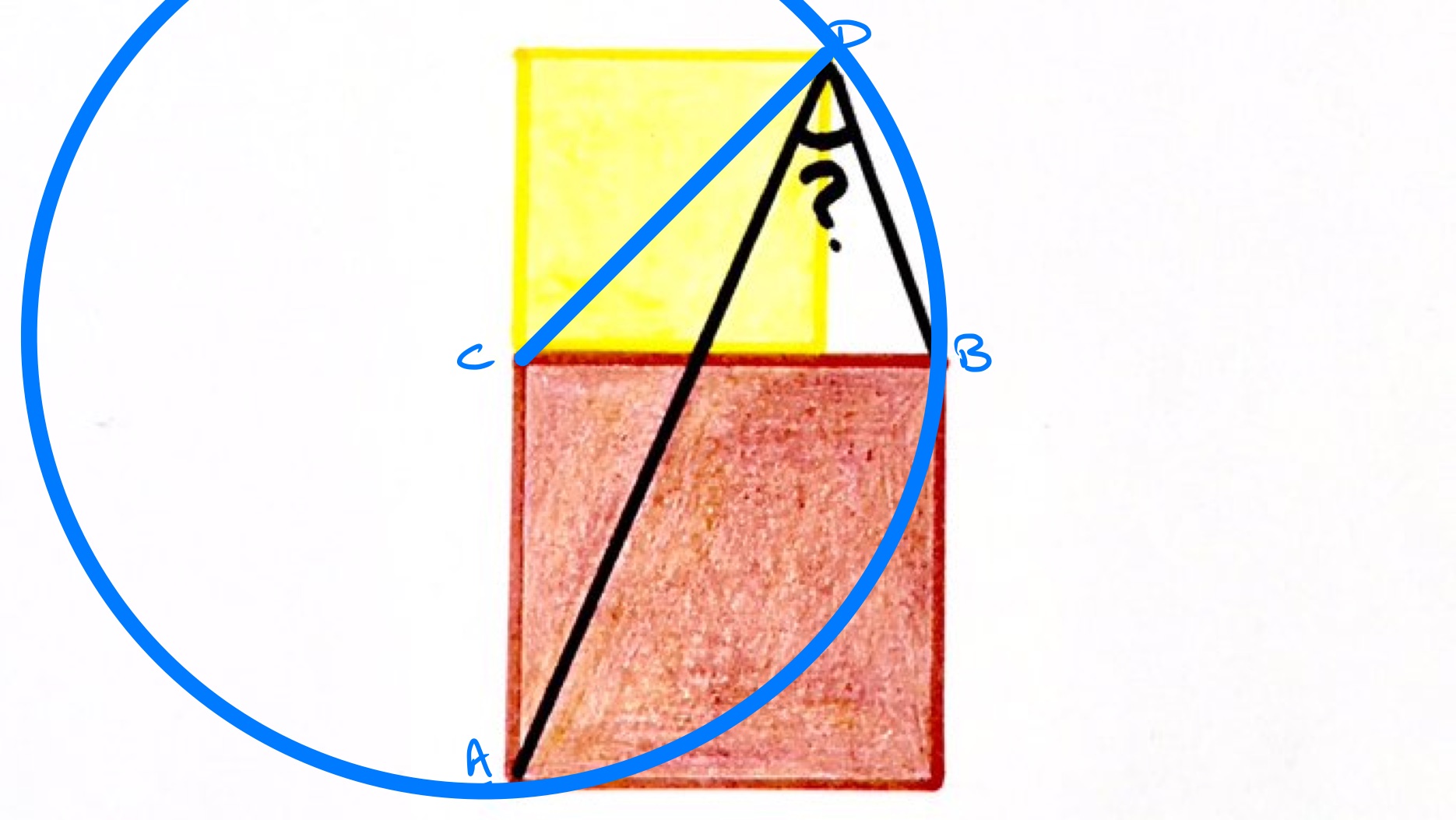
As the red square has double the area of the yellow square, the length of the diagonal of the yellow square is the same as the side length of the red square.
This means that a circle drawn with centre through also passes through and . Then as the angle at the circumference is half the angle at the centre, angle is half of , which is . So angle is .
Solution by Properties of Squares, Isosceles Triangle, and Angles in a Triangle
As above has the same length as so triangle is isosceles. Since angle is , this means that angle is . Triangle is also isosceles and angle is so angle is . This makes angle equal to .