Notes
two squares overlapping a third square solution
Solution to the Two Squares Overlapping a Third Square Puzzle
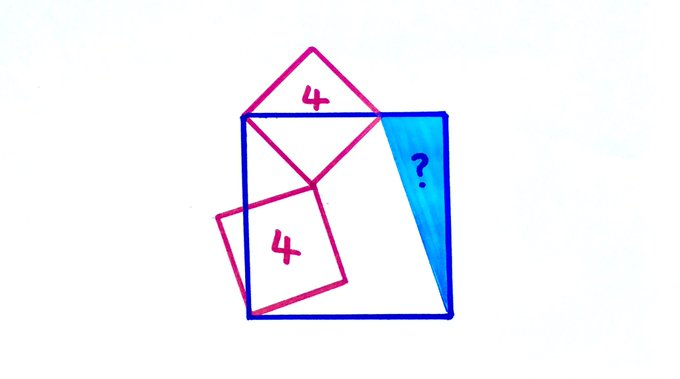
Two of these three squares have area . What’s the area of the blue triangle?
Solution by Lengths in Equilateral Triangles and Lengths in Squares
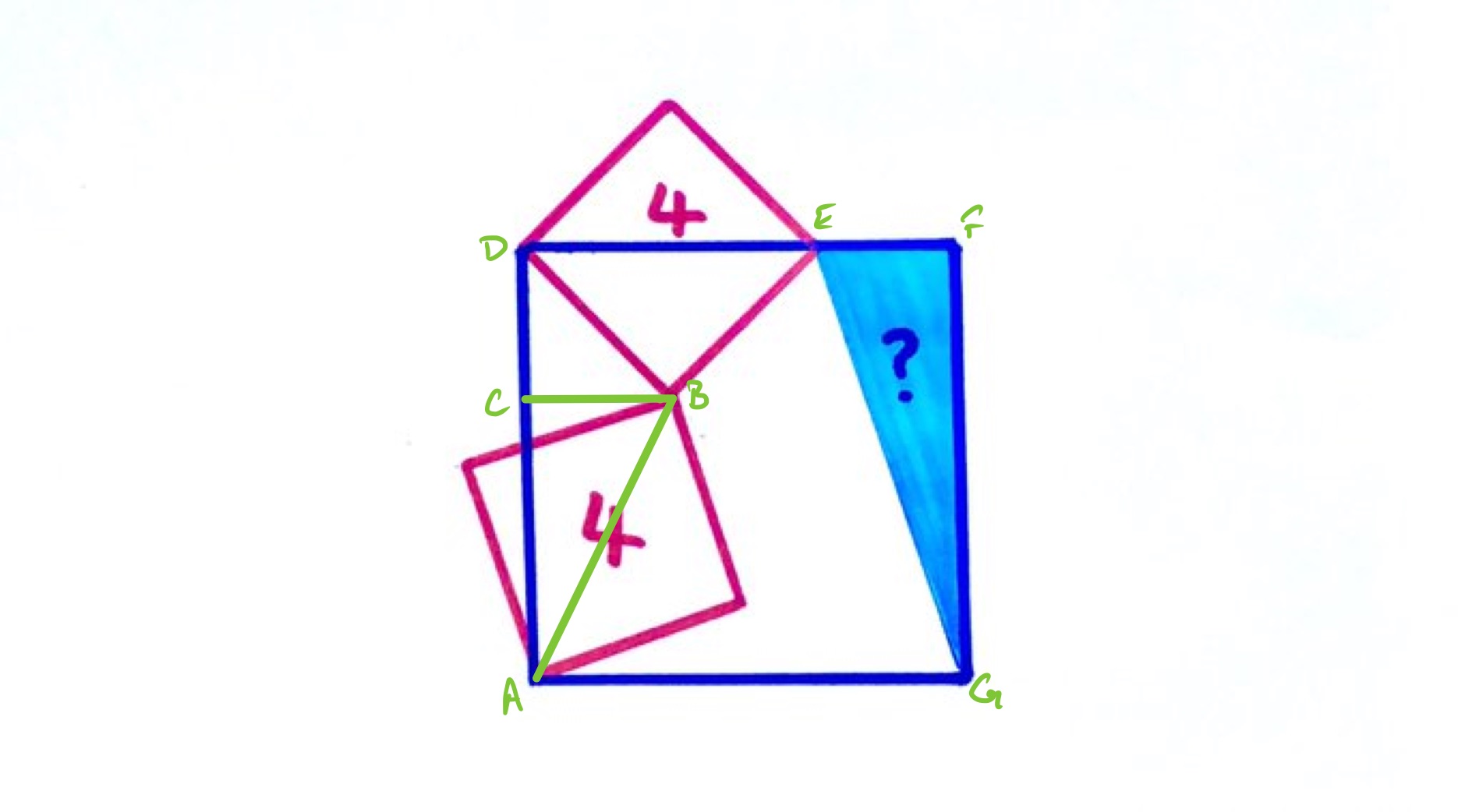
In the above diagram, the point labelled is directly across from , so that angle is a right-angle. As the red squares have area , they have side length and diagonal .
The length of line segment is half of a diagonal of the red squares, namely , so triangle is a right-angled triangle with one side half of the hypotenuse. This means that it is half of an equilateral triangle and so has length times the length of , so has length . Since also has length , the full length of the side of the outer square is .
The length of is then . The area of triangle is therefore: