Notes
two squares overlapping a square solution
Solution to the Two Squares Overlapping a Square Puzzle
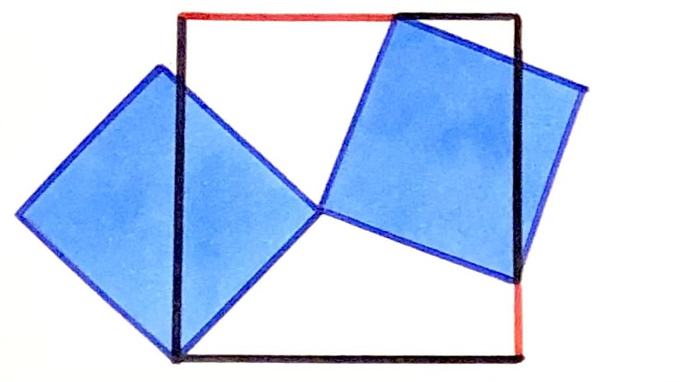
Three squares. The blue ones each have area 18. What’s the sum of the red lengths?
Solution by Congruent Triangles
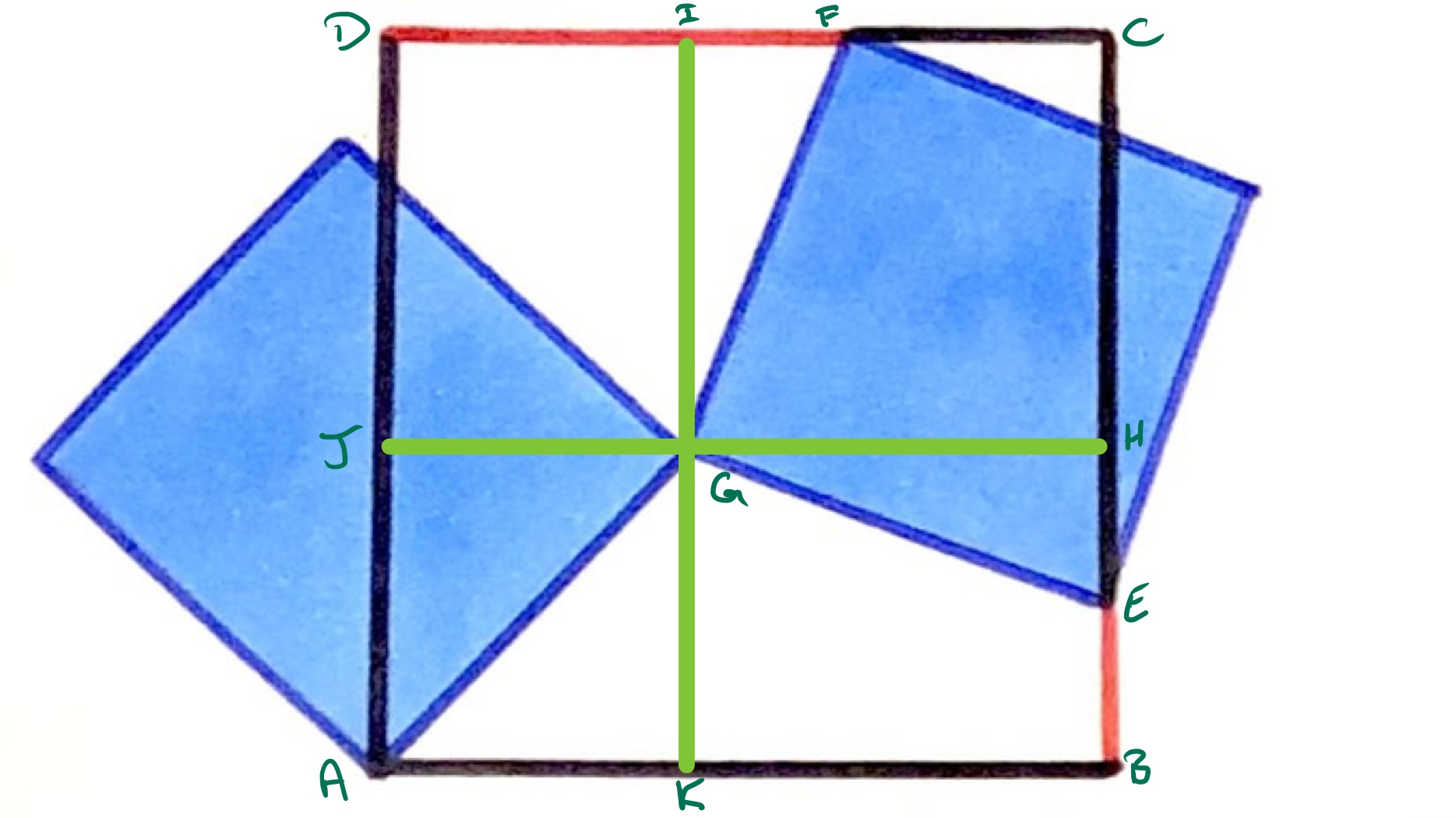
In the above diagram, the lines and are the vertical and horizontal lines through , respectively.
The angles and are the same, since both are equal to , and the lengths of and are the same, so triangles and are congruent. This means that and have the same length as each other, so also and have the same length as each other.
Also from the congruence, and have the same length, so the sum of the lengths of and is the length of and so also of . The remainder of is which has the same length as . So the lengths of the red lines have the same sum as the lengths of and .
Now and are equal and perpendicular meaning that is actually at the centre of the left-hand square. The quadrilateral is therefore a square of area half that of the left-hand square, and so of area . It therefore has side length so the sum of the red lines is .
Solution by Invariance principle
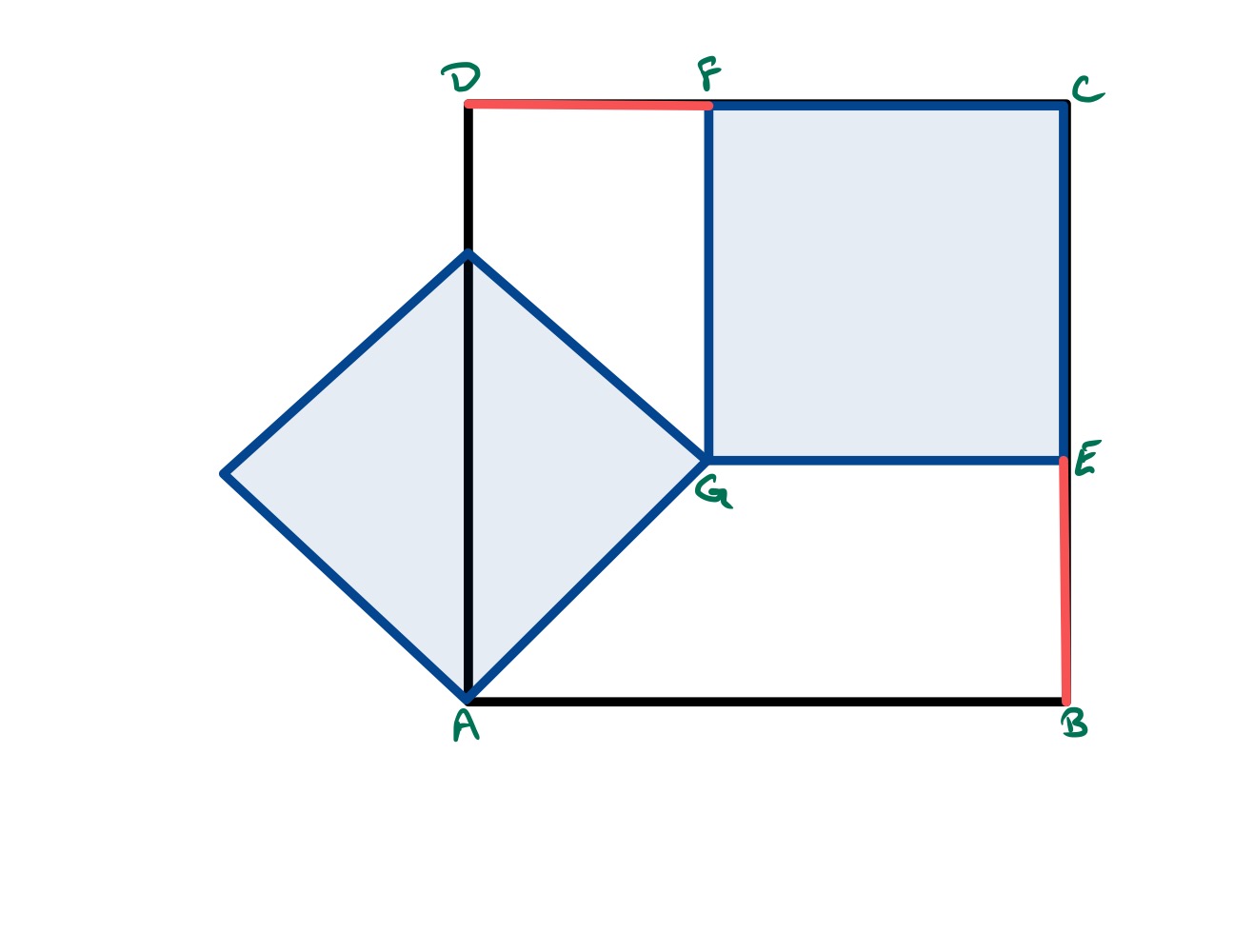
The property that can vary in this diagram is the angle of the right-hand square. Drawing it so that it is oriented the same as the outer square puts it in the right-hand top corner of that square. That and are the sides of a square with diagonal is then obvious.