Notes
two squares overlapping a square ii solution
Solution to the Two Squares Overlapping a Square Puzzle
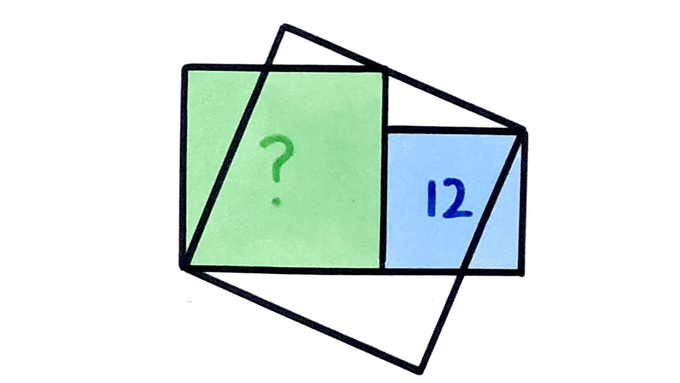
Three squares. What’s the green area?
Solution by Similar Triangles
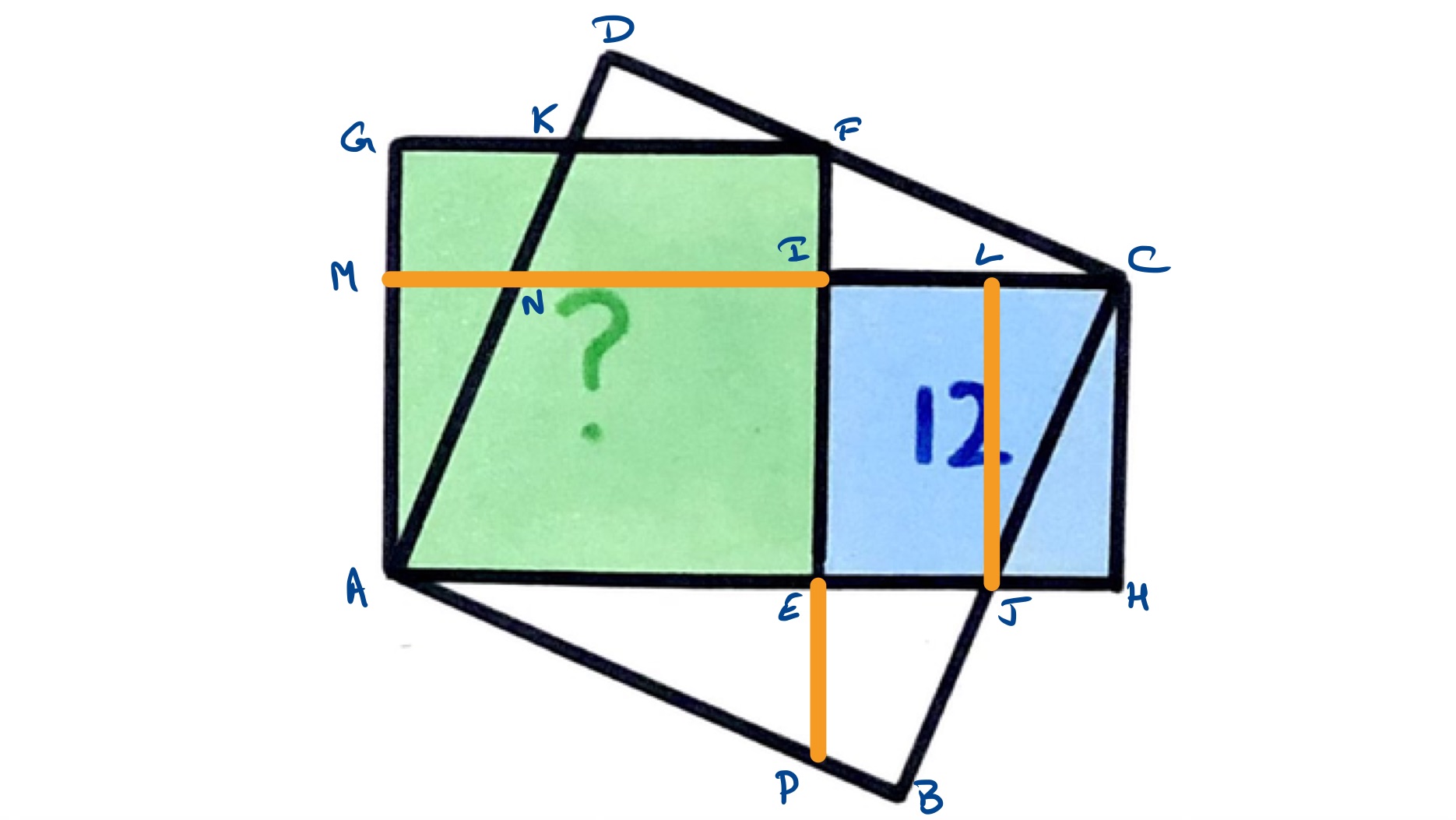
The starting point of this strategy is to consider the rectangle . The triangles and are congruent, so the lengths of and are the same. The side of the longer square is therefore the same as the side of the shorter square plus the length of . As is the side of the shorter square without , the segment has length twice the side of the shorter square. The area of is therefore double that of the smaller square, hence .
Comparing this with the larger square, we have rectangle too much and too little. The areas of these rectangles are given by and . We can replace by and by .
Triangles and are congruent, so the lengths of and are the same. The lengths of and are the same, so and have the same length, then as triangles and are congruent, so and have the same length. So we can replace by and by . The areas of the two rectangles are therefore equal to and .
The triangles and are similar, meaning that . Rearranging this shows that and so that the two rectangles and have the same area. This means that the green square has the same area as the rectangle , which is .
Solution by Angle at the Centre is Twice the Angle at the Circumference
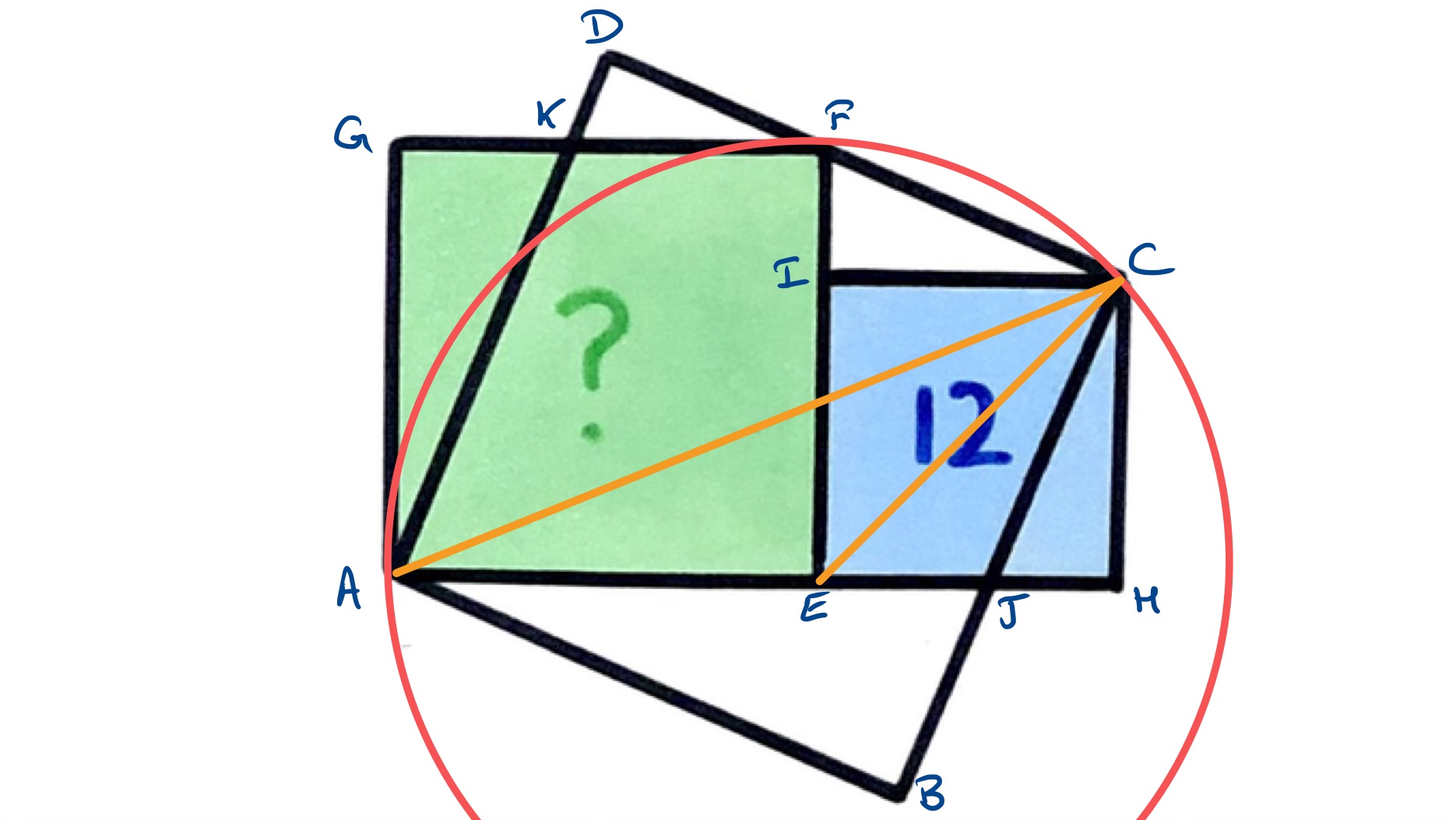
Consider the circle centred at the point that passes through and (as is a square, the lengths of and are equal so the circle does pass through both).
The angle is a right-angle, as it is the corner of a square. The angle is , as it is between a diagonal and side of a square. Therefore, by the result that the angle at the centre is twice the angle at the circumference, lies on the circle centred at . The segment is therefore a radius of this circle and so the length of is the same as that of . As is a diagonal of the smaller square, the square with side has area twice that of the smaller square and so the area of the green square is .