Notes
two squares overlapping a semi-circle solution
Two Squares Overlapping a Semi-Circle
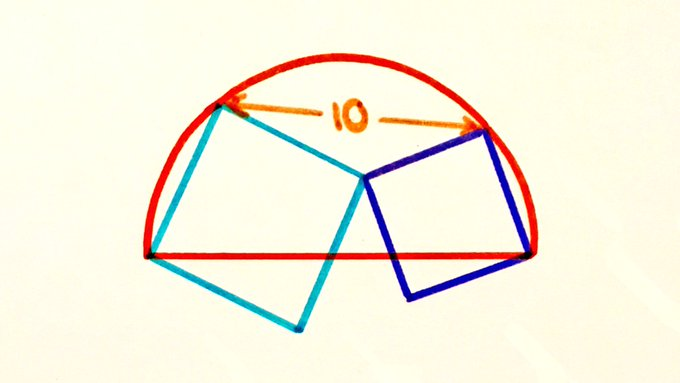
Find the area of the semicircle. (Blue shapes are squares)
Solution by Angle in a Semi-Circle, Vertically Opposite Angles, and Similar Triangles
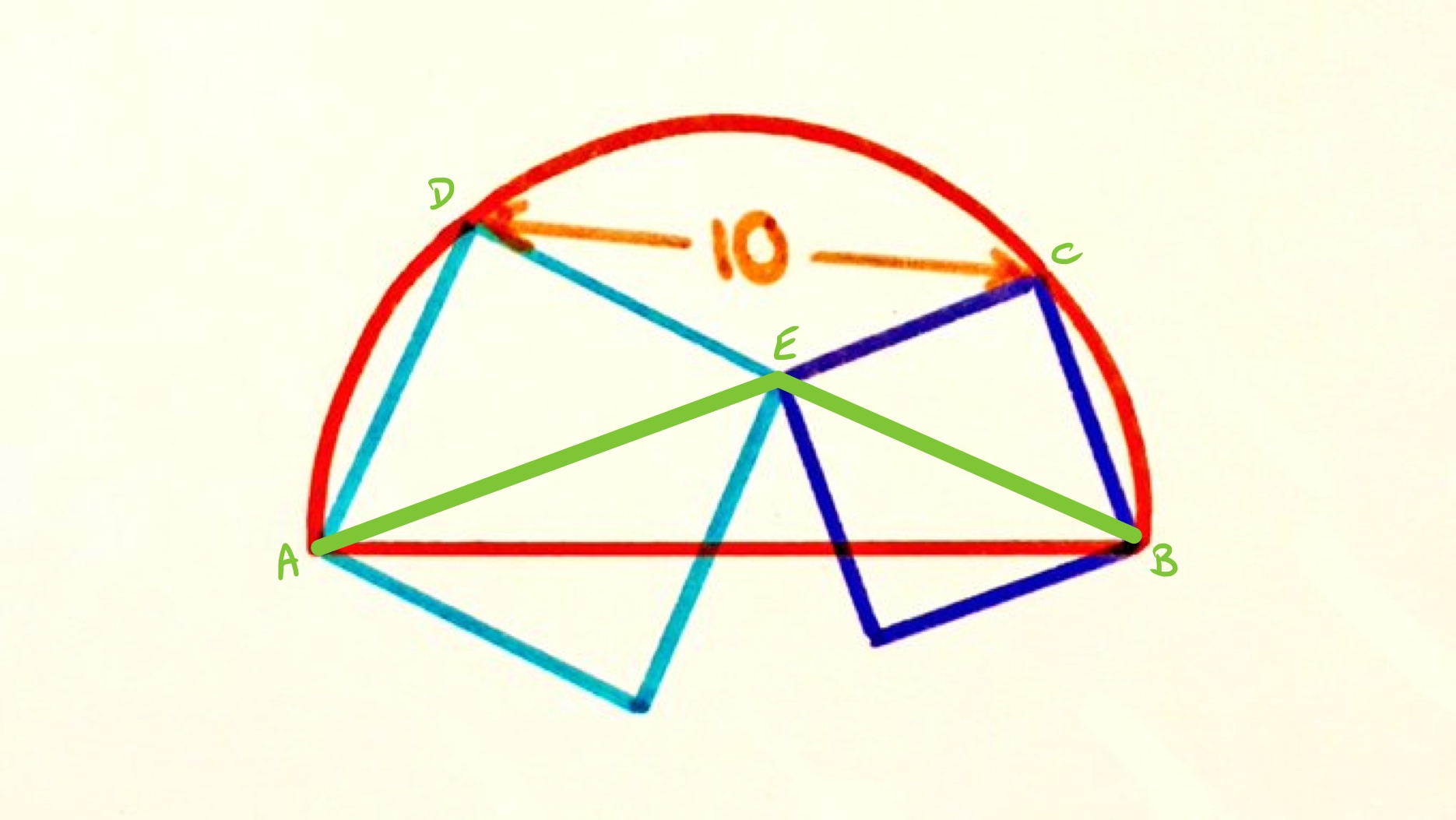
With the points labelled as in the above diagram, the direct line from to forms a right-angle with the line since this is the angle in a semi-circle. Since is also at right-angles to , this means that is an extension of , so is a straight line. Similarly, is a straight line.
Since vertically opposite angles are equal, angles and are equal. Then is a diagonal of a square of which is a side, and is a diagonal of a square of which is a side. Put together, these mean that triangle is similar to triangle with scale factor . The length of is therefore and so the area of the semi-circle is .