Notes
two squares on a circle solution

Solution to the Two Squares on a Circle Puzzle

Solution by Angle in a Semi-Circle and Pythagoras' Theorem

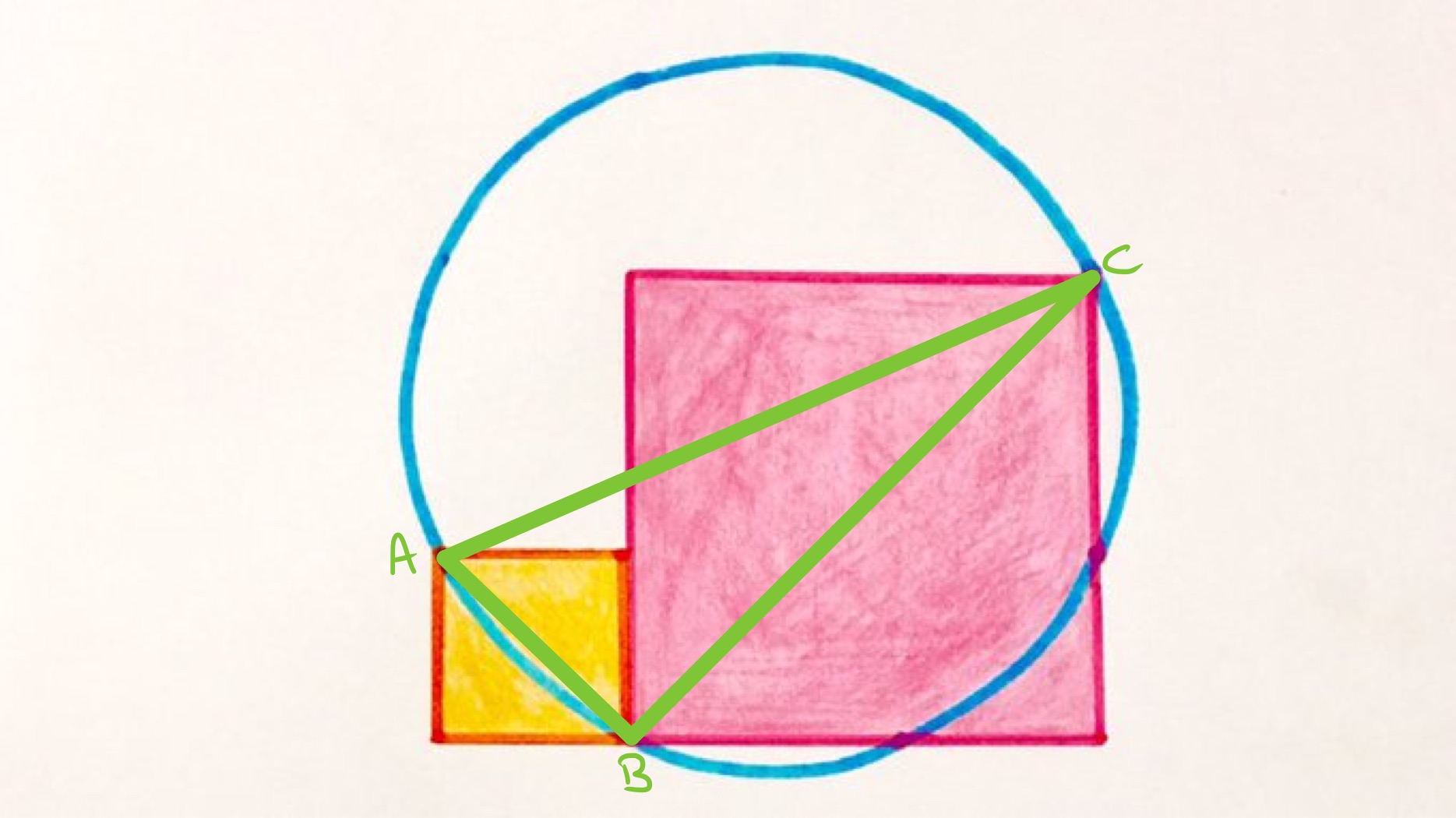
In the above diagram, angle $C \hat{B} A$ is a right-angle, so as the angle in a semi-circle is a right-angle, $A C$ must be a diameter of the circle. It therefore has length $8$. Let the squares have side lengths $a$ and $b$, with $a$ of the yellow square and $b$ of the pink. Then $A B$ has length $a\sqrt{2}$ and $B C$ has length $b\sqrt{2}$. Applying Pythagoras' theorem to triangle $A B C$ shows that:

So $a^2 + b^2 = 32$. Since the areas of the squares are $a^2$ and $b^2$, this shows that the combined area of the two squares is $32$.