Notes
two squares inside a semi-circle solution

Solution to the Two Squares Inside a Semi-Circle Puzzle

Solution by angle in a semi-circle

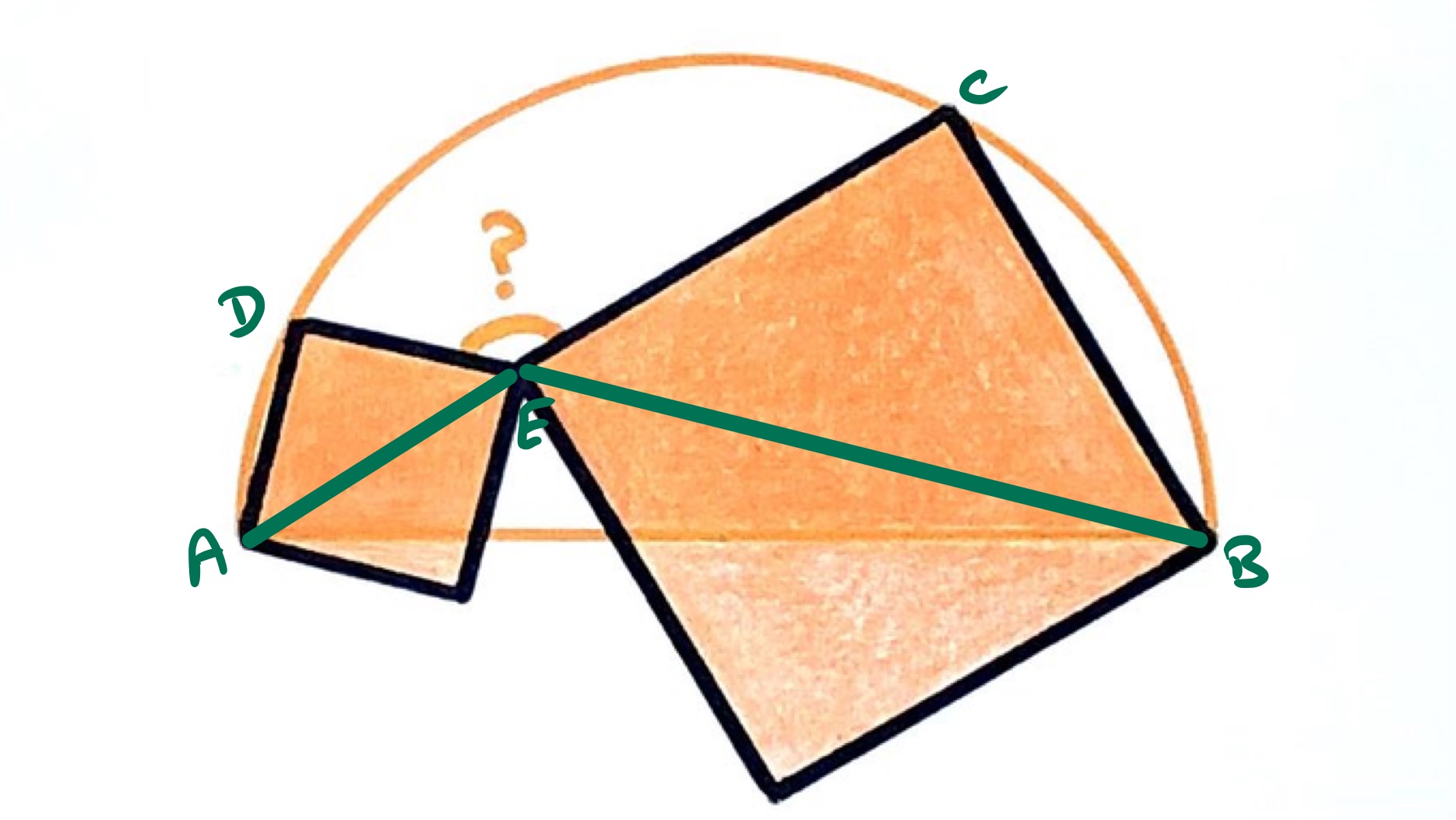
Consider the diagonals of the squares, as in the above diagram. The claim is that the lines $D E B$ and $A E C$ are straight lines. To see this, consider the triangle $A D B$. The point $D$ is on the circumference of the circle of which $A B$ is a diameter, so by angles in a semi-circle, angle $A \hat{D} B$ is a right-angle. Since angle $A \hat{D} E$ is also a right-angle, the line segments $D B$ and $D E$ must overlap and hence $A E B$ is a straight line. The same argument shows that $A E C$ is a straight line.

This means that angle $B \hat{E} C + C \hat{E} D = 180^\circ$, and then since $E B$ is the diagonal of a square, $B \hat{E} C = 45^\circ$ leading to $C \hat{E} D = 135^\circ$.