Notes
two squares in a triangle solution
Solution to the Two Squares in a Triangle Puzzle
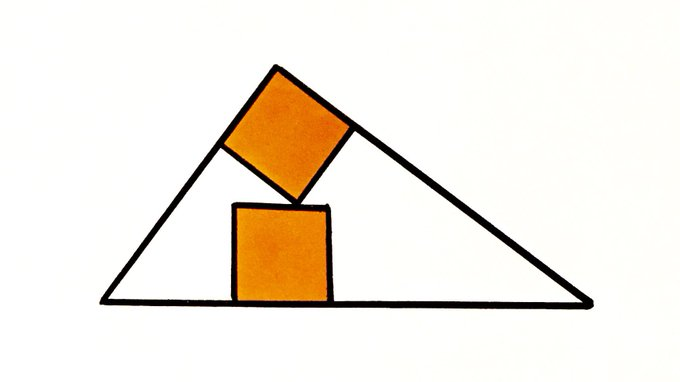
The perimeter of each square is of the perimeter of the triangle. What fraction is shaded?
Solution by Area of a Triangle
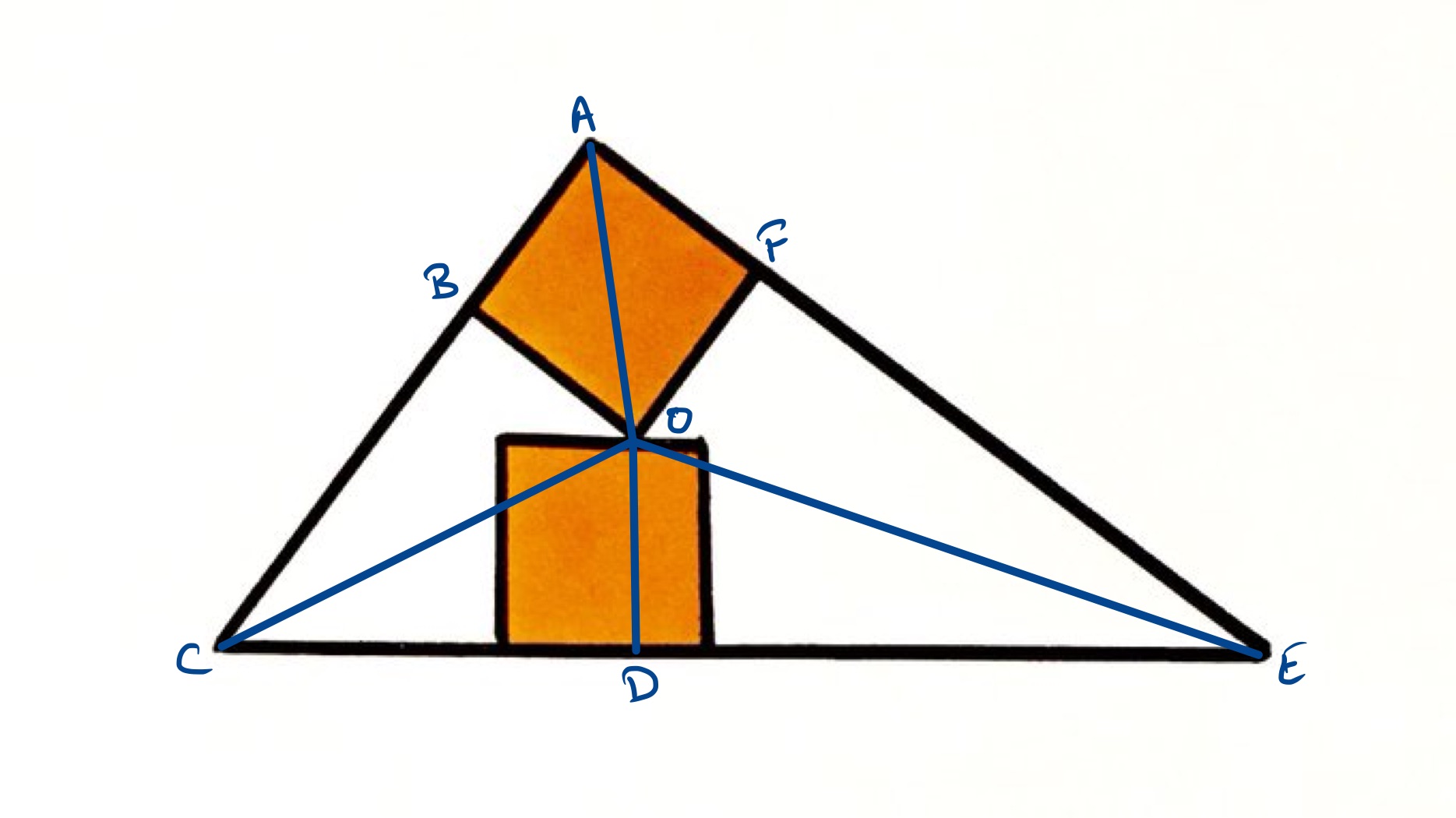
Let denote the length of the side of one of the squares. The point in the above diagram has the property that , , and are all perpendicular to the sides of the triangle that they meet, and are all of the same length, namely . Dividing the triangle into three by cutting from each vertex to shows that the area of the triangle is the same as that of three triangles each with height and whose collective bases sum to the perimeter of the original triangle, which is given as . Therefore the area of the triangle is , while the shaded region has area . The fraction that is shaded is then .