Notes
two squares in a semi-circle solution
Solution to the Two Squares in a Semi-Circle Puzzle
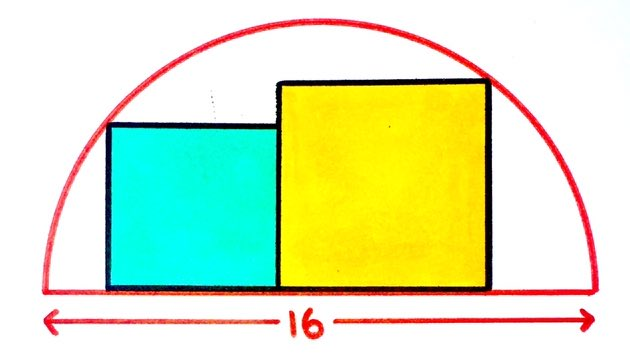
What’s the total area of these two squares?
Solution by Pythagoras' Theorem, Properties of Chords, and Isosceles Right-Angled Triangles
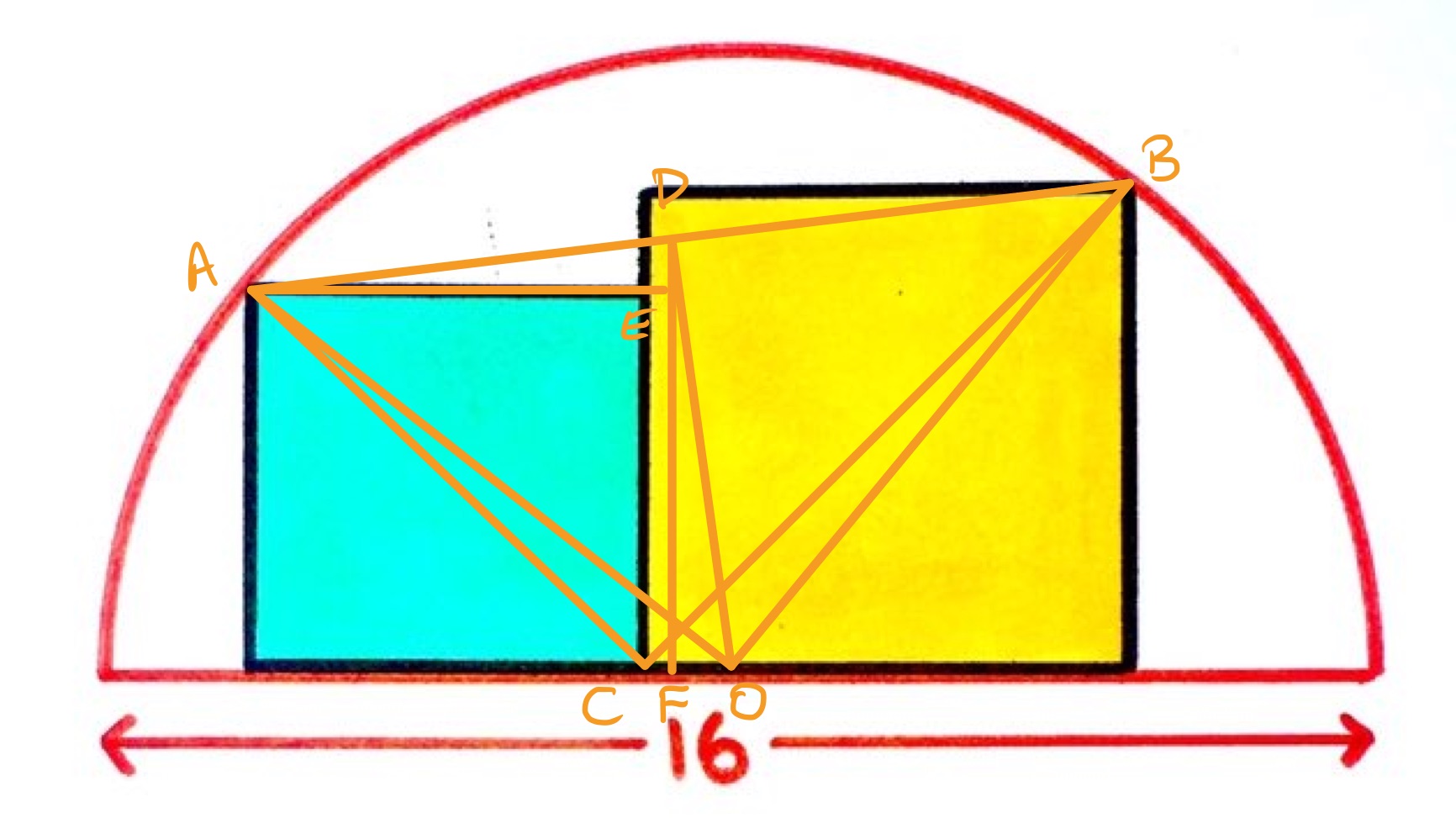
In the above diagram, the point labelled is the centre of the circle and is the midpoint of the chord . Point is directly below , and is where the horizontal from meets the vertical from . Let be the length of a side of the blue square and of the yellow square.
The horizontal distance from to is , so the length of is . The height of above the diameter is the average of the heights of and , so also is . As the perpendicular bisector of a chord passes through the centre of the circle, angle is a right-angle. This means that angles and add up to so triangles and are similar. Since and have the same length, they are actually congruent. This means that and are also the same length. Triangle is therefore isosceles, as is triangle , and so triangle is a right-angled isosceles triangle. The length of is the radius of the semi-circle, which is , so the square of the length of is .
Triangle is also right-angled with of length and of length . Applying Pythagoras' theorem to this triangle gives:
which gives the total area of the squares as .
Solution by Invariance Principle
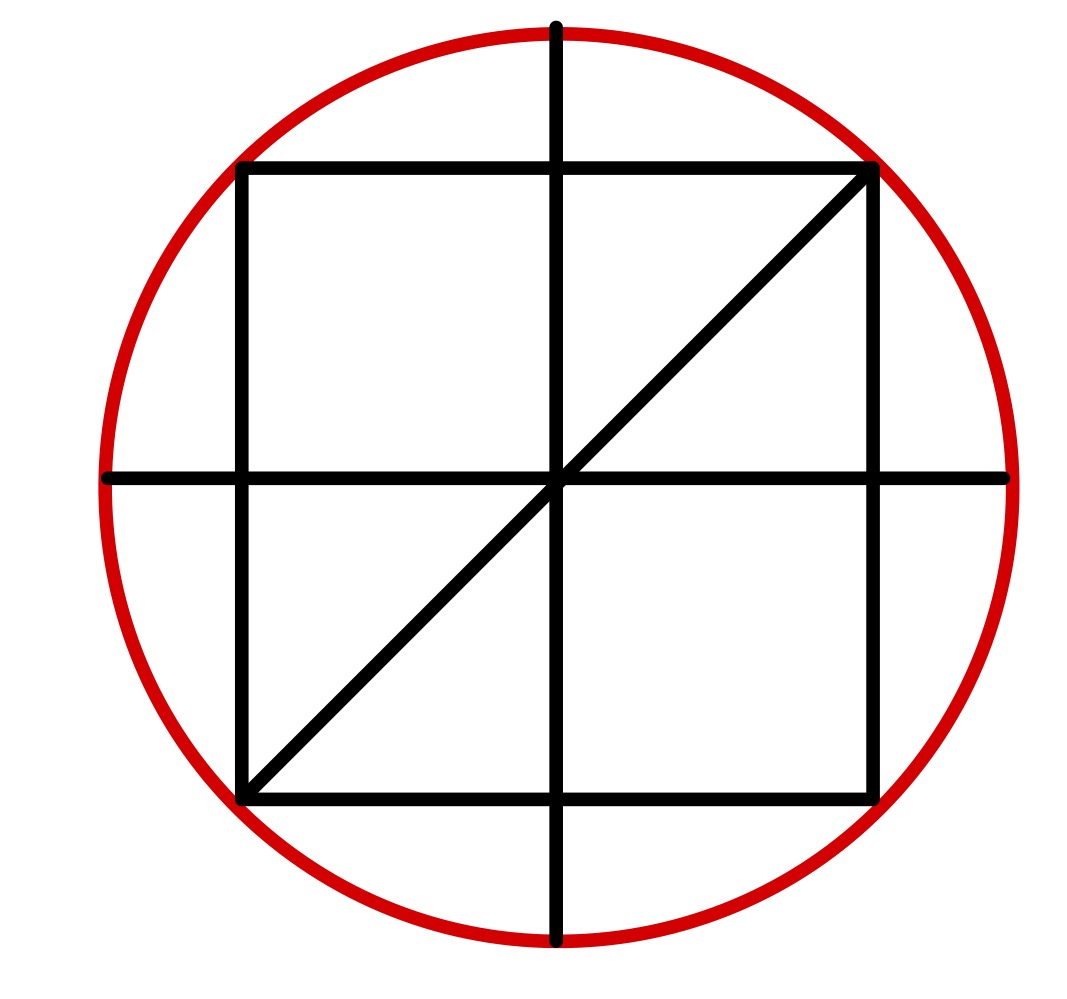
In this special case, the two squares are drawn to be the same size. The diagonal of one of the squares is a radius of the circle, so is of length . The side length is therefore and so each has area . The total area is then .