Notes
two squares diagonally inside a rectangle solution
Solution to the Two Squares Diagonally Inside a Rectangle Puzzle
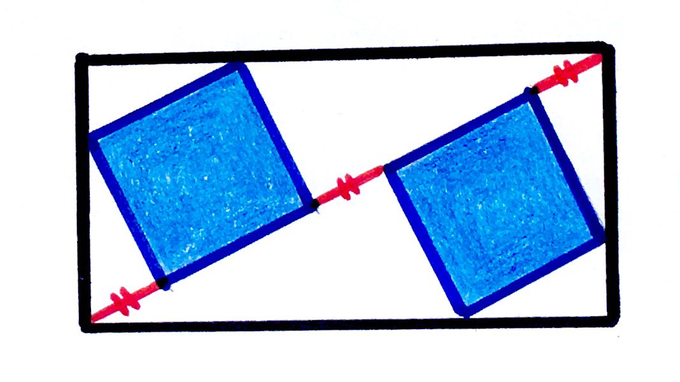
Two squares sit on the diagonal of the rectangle. The red sections of the diagonal are equal length. What fraction of the rectangle is shaded?
Solution by Similar Triangles
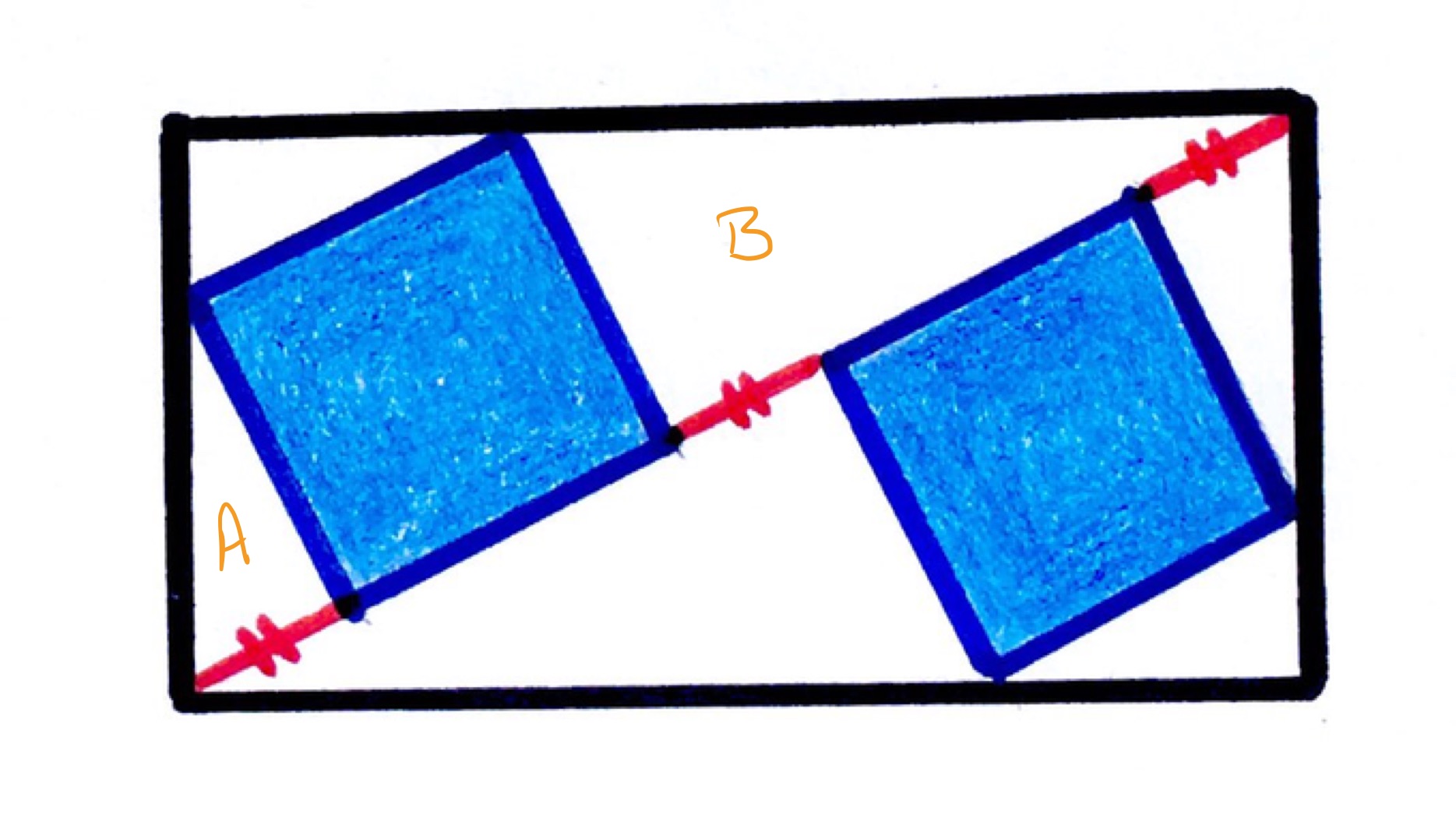
Let be the length of a red segment and the length of a side of the square. The triangles labelled and are similar, so the ratios and are equal. This means that . This has solution (the other possible solution is but and are both lengths). The ratio of the lengths of the shorter sides of these triangles is then .
The diagonal of the rectangle is then .
Consider a half rectangle. This is then a right-angled triangle similar to the others so its shorter sides are in the ratio . To compute its height (in order to then calculate its area) consider the following diagram in which triangles and are right-angled triangles with shorter sides of lengths in ratio .
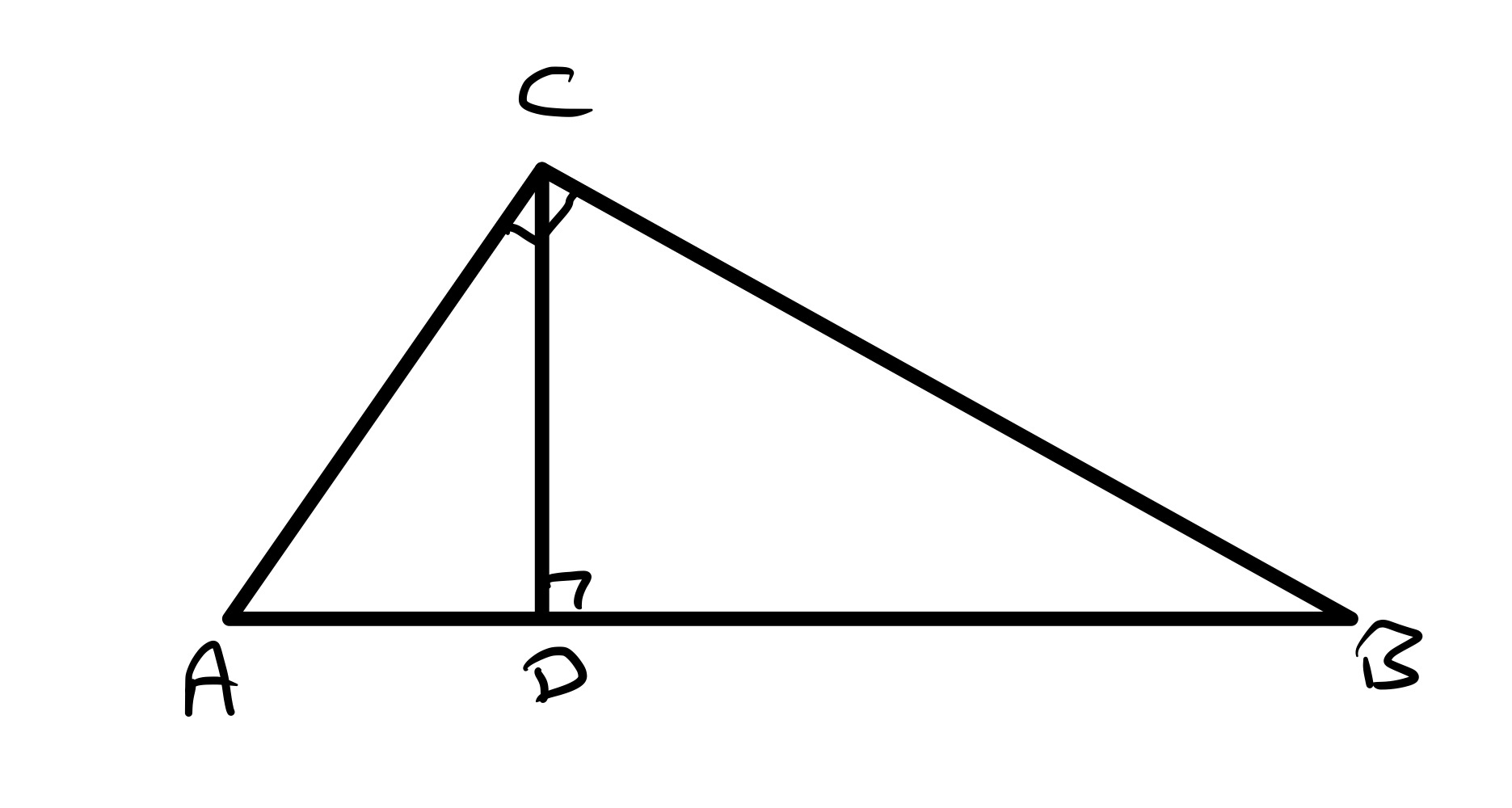
Then the ratio of the lengths of to is so the ratio of to is .
So the height of the half rectangle is and so its area is . The combined area of the blue squares is . So the fraction of the rectangle that is shaded is .