Notes
two squares and two equilateral triangles ii solution
Solution to the Two Squares and Two Equilateral Triangles II Puzzle
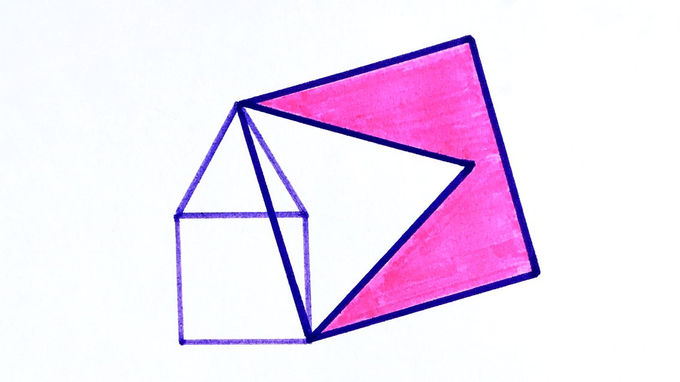
Two squares and two equilateral triangles. If the area of the smaller square is , what’s the shaded area?
Solution by Properties of Equilateral Triangles and Pythagoras' Theorem
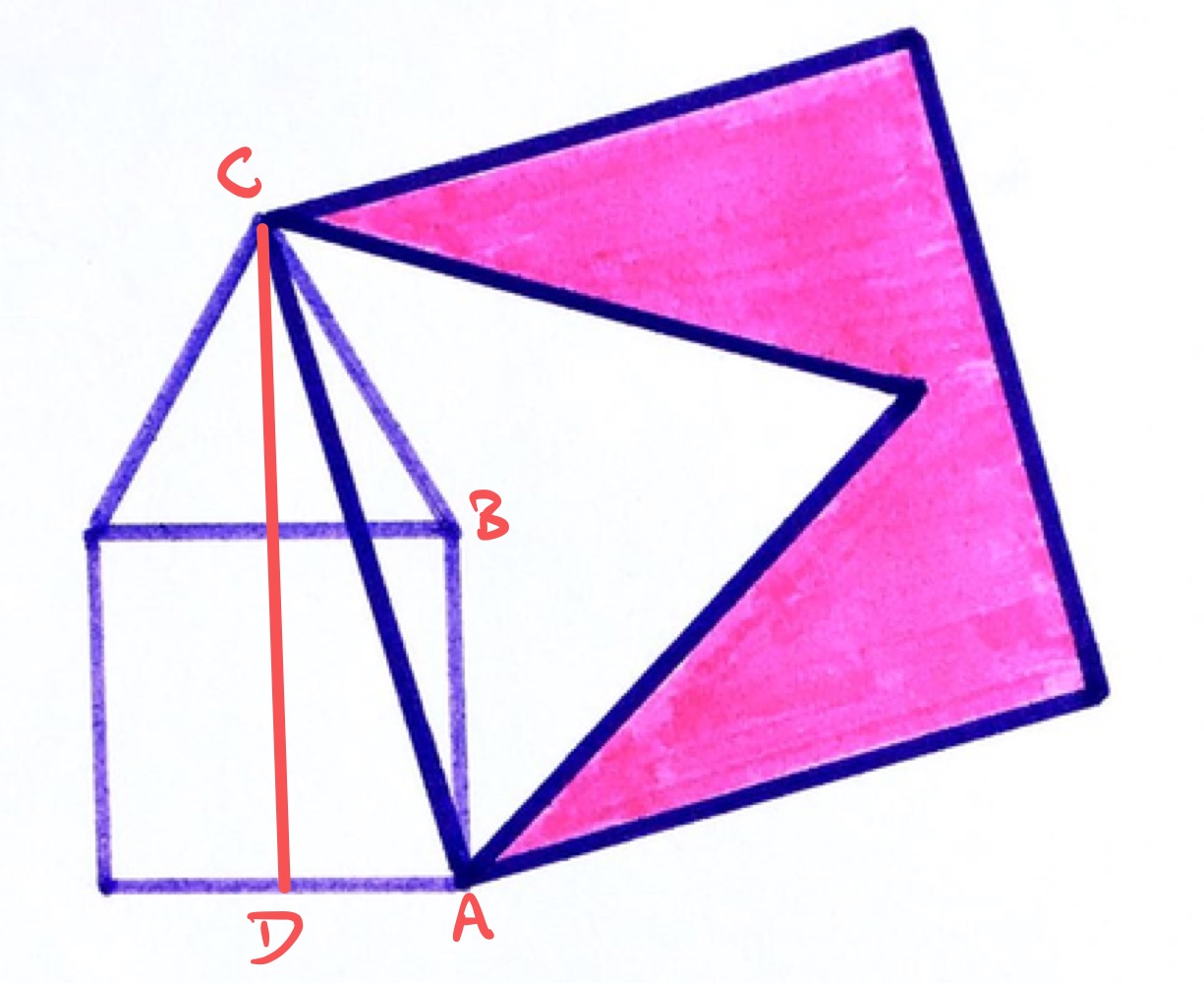
In the diagram above, the point is such that is perpendicular to the base of the square.
As the square has area , its side length is , so the length of line segment is . From the lengths in an equilateral triangle, line segment has length .
Applying Pythagoras' theorem to triangle shows that the length of is:
The area of the large square is therefore , and the area of the large equilateral triangle is times this, so the area of the pink region is: