Notes
two squares and an equilateral triangle solution
Two Squares and an Equilateral Triangle
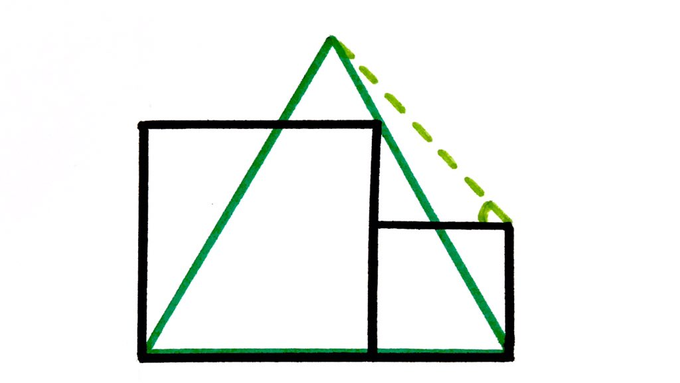
Two squares and an equilateral triangle. What’s the angle?
Solution by Equations of Lines
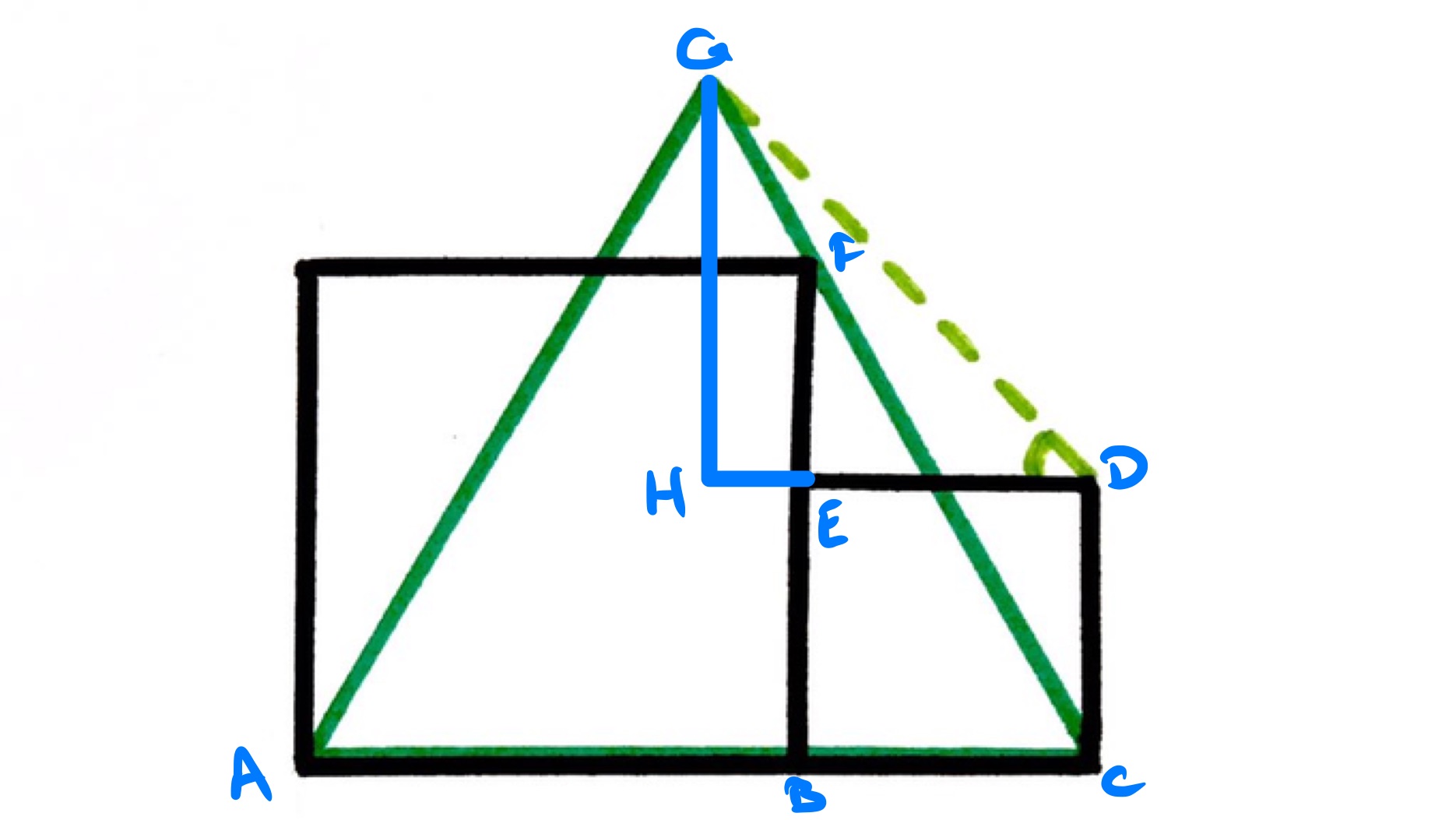
Position the diagram on a coordinate grid so that point is at the origin and point at the point . From the properties of equilateral triangles, the coordinates of can be seen to be and so the equation of the line extending is:
Point lies on this line and also on the line . Its coordinates can therefore be calculated to be .
The length of is then and so the coordinates of are . The length of is therefore:
The triangle is therefore an isosceles right-angled triangle and so angle is .