Notes
two squares and a semi-circle solution
Solution to the Two Squares and a Semi-Circle Puzzle
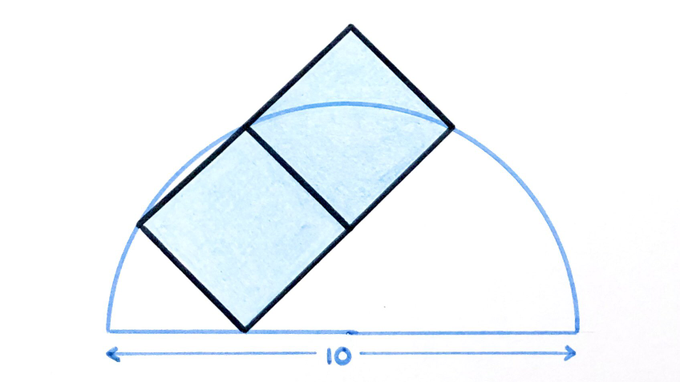
What’s the total area of these two squares?
Solution using Chords and Pythagoras' theorem
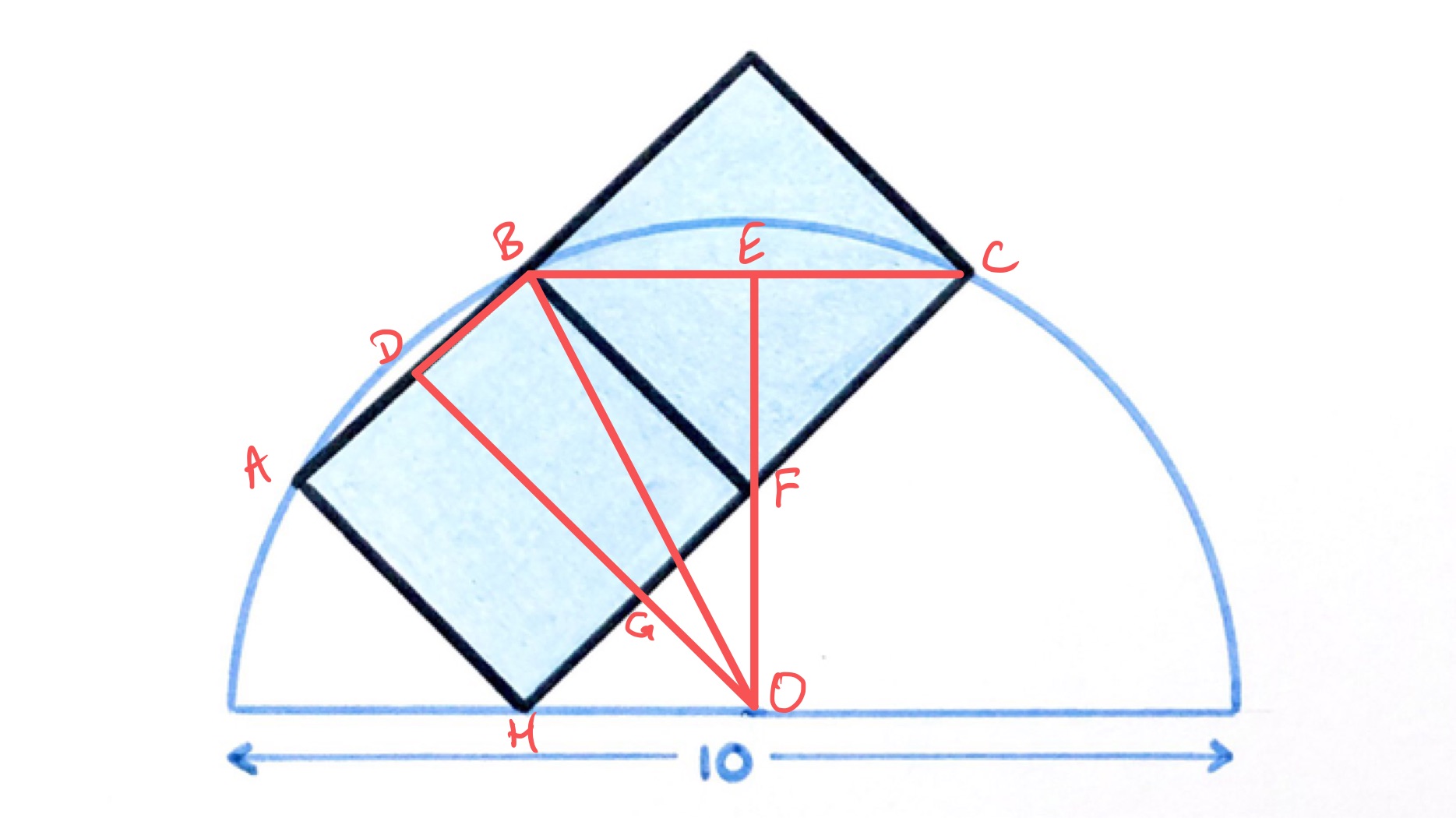
The centre of the circle lies on the perpendicular bisectors of the chords and . The perpendicular bisector of passes through its midpoint and the corner while that of passes through and . Triangle is a right-angled isosceles triangle that is congruent to . This establishes has having the same length as the half side, . So is three times the length of .
Let be the length of , then had length and has length . Since the length of is , Pythagoras' theorem applied to triangle establishes that:
The total area of the squares is then .