Notes
two squares and a quarter circle solution
Solution to the Two Squares and a Quarter Circle Puzzle
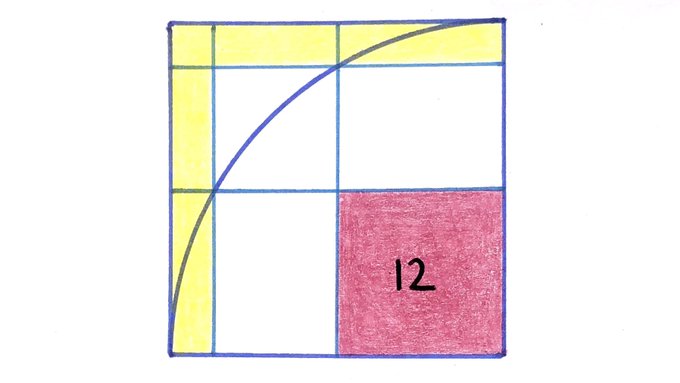
The area of the red square is 12. What’s the total yellow area?
Solution by Pythagoras' Theorem and the Area of a Square
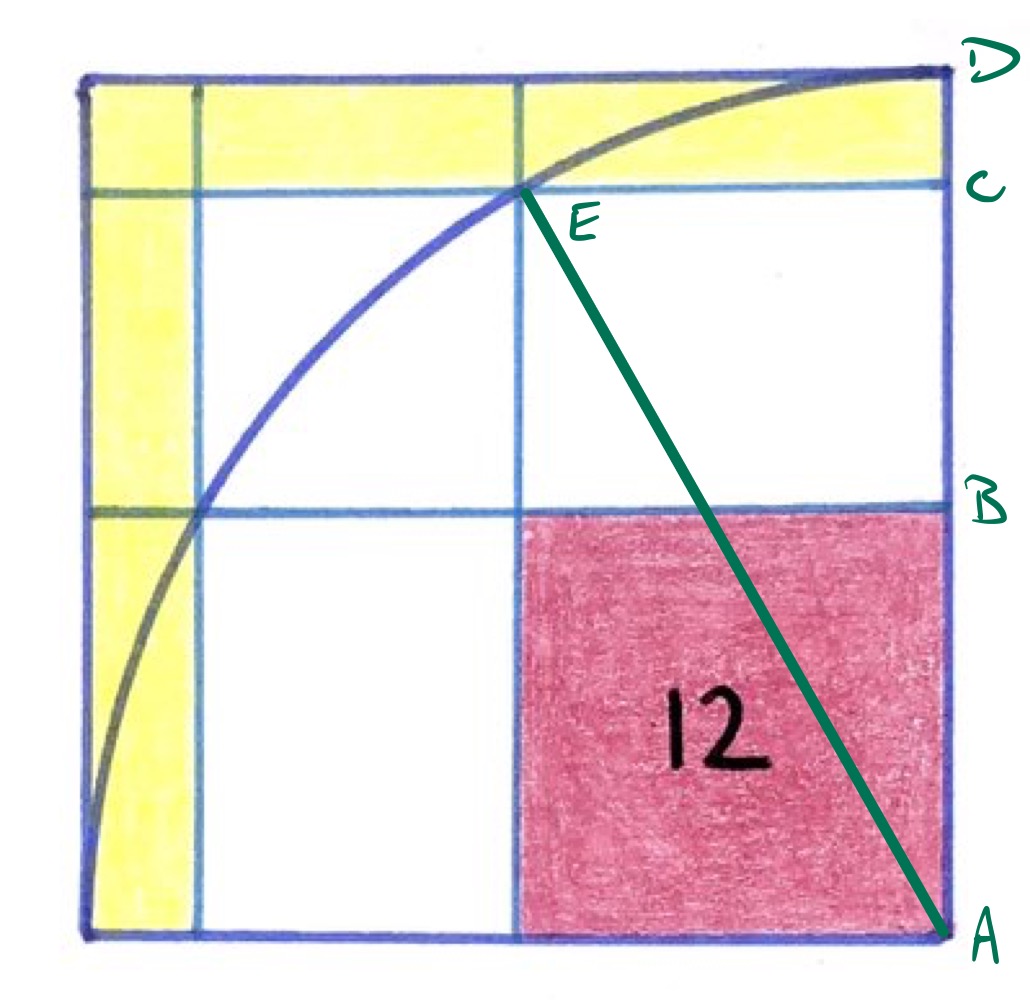
Consider the diagram as labelled above.
The red square has area , so its side length is . Let be the radius of the quarter circle, so is the length of line segment . The length of line segment can then be found using Pythagoras' theorem:
The area of the outer square is , so the yellow area is:
Solution by Invariance Principle and Lengths in a Square
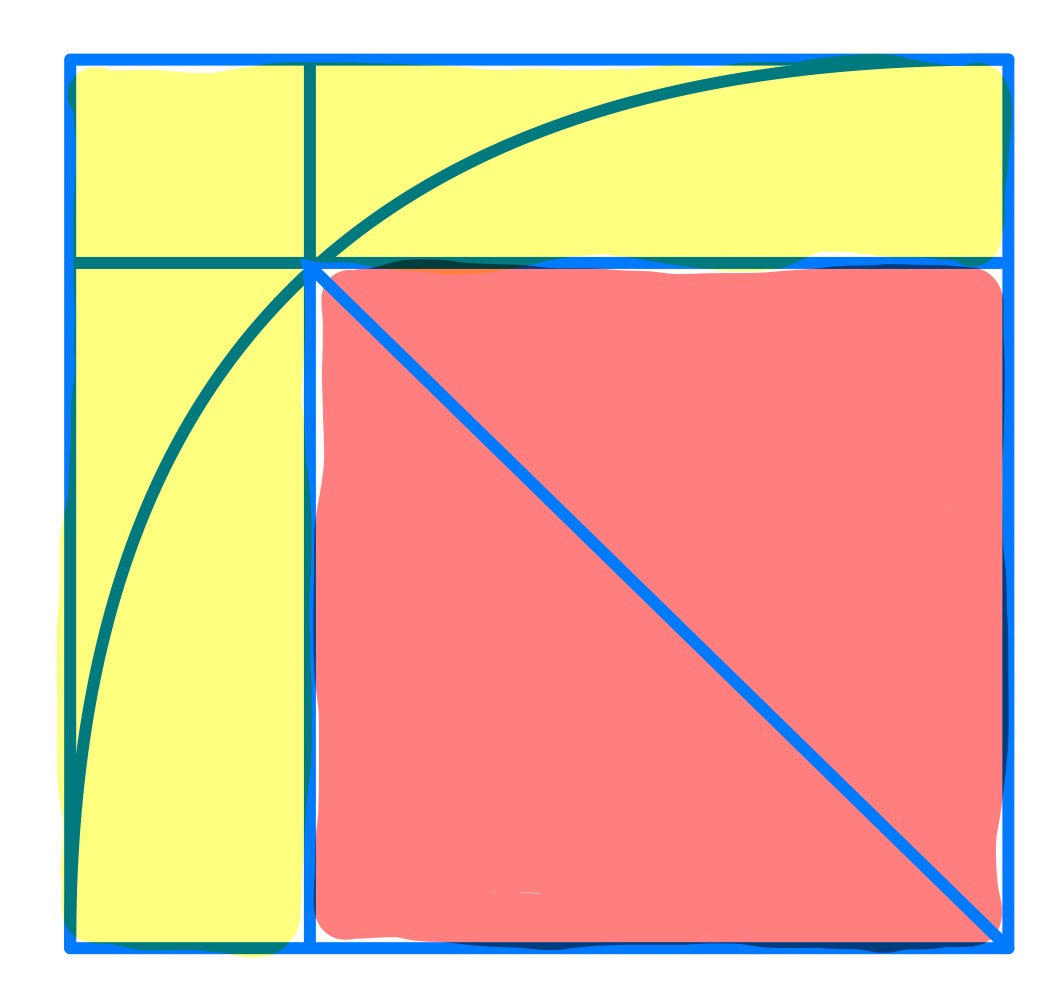
The radius of the quarter circle is not fixed, so can be varied. At one extreme, the white area shrinks to non-existence.
The radius of the quarter circle is the diagonal of the red square, and so has length times the side length of the square. The outer square therefore has double the area of the red square, and so the area of the yellow region is the same as that of the red square, namely .