Notes
two semi-circles inside a semi-circle solution
Two Semi-Circles Inside a Semi-Circle
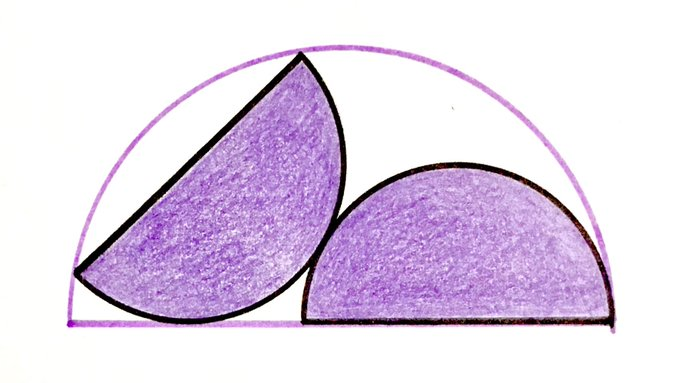
The two shaded semicircles are the same size. What fraction of the larger semicircle do they cover?
Solution by Angle Between a Radius and Tangent, Pythagoras' Theorem, and Properties of Chords
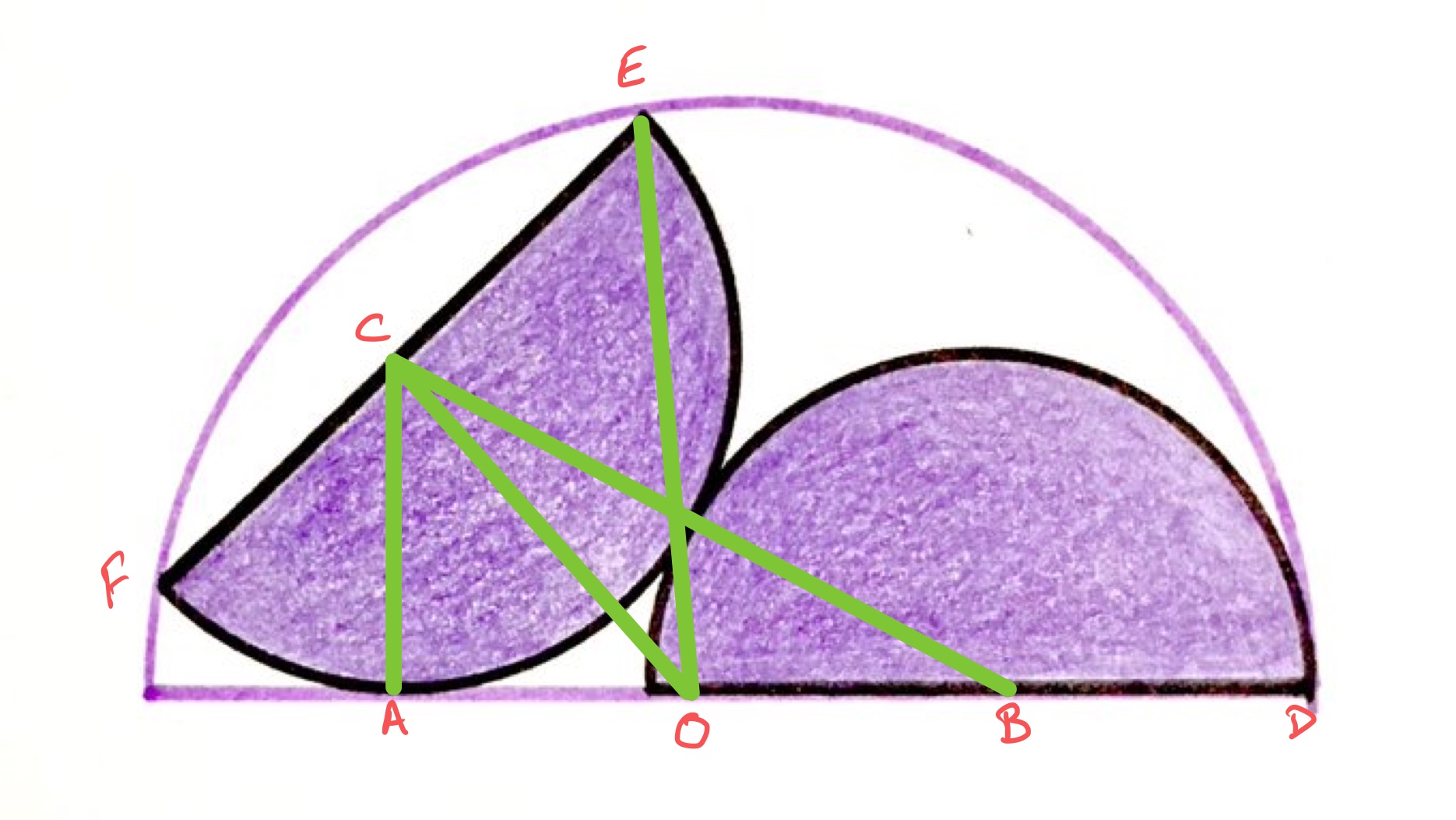
In the above diagram, point is the centre of the larger semi-circle while points and are the centres of the shaded ones. Let be the radius of the smaller semi-circles and the radius of the largest one. Then is the length of and of , while has length . Both and have length .
As is tangent to the left-hand semi-circle, angle is since it is the angle between a radius and tangent. Therefore, triangle is right-angled and applying Pythagoras' theorem to it shows that has length . Then has length and so has length .
Applying Pythagoras' theorem to triangle shows that the length of is given by:
Since is a chord of the outer semi-circle, and is its midpoint, the line is perpendicular to and so triangle is right-angled. Applying Pythagoras' theorem to this yields the equation:
The area of the larger semi-circle is therefore . The shaded area is . Therefore the fraction that is shaded is .