Notes
two semi-circles inside a semi-circle ii solution
Solution to the Two Semi-Circles Inside a Semi-Circle II Puzzle
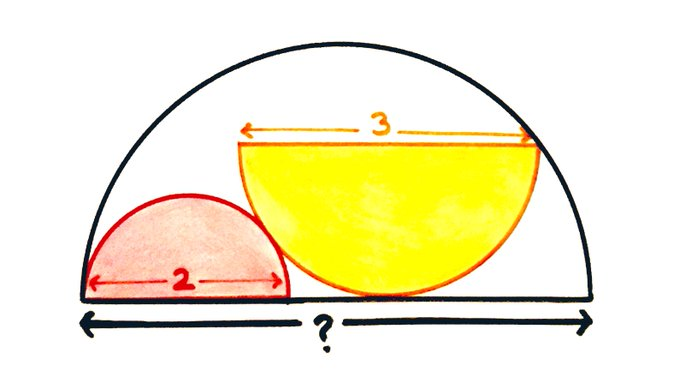
What’s the diameter of the largest semicircle?
Solution by Angle Between a Radius and Tangent, Pythagoras' Theorem, Angle in a Semi-Circle, and Similar Triangles
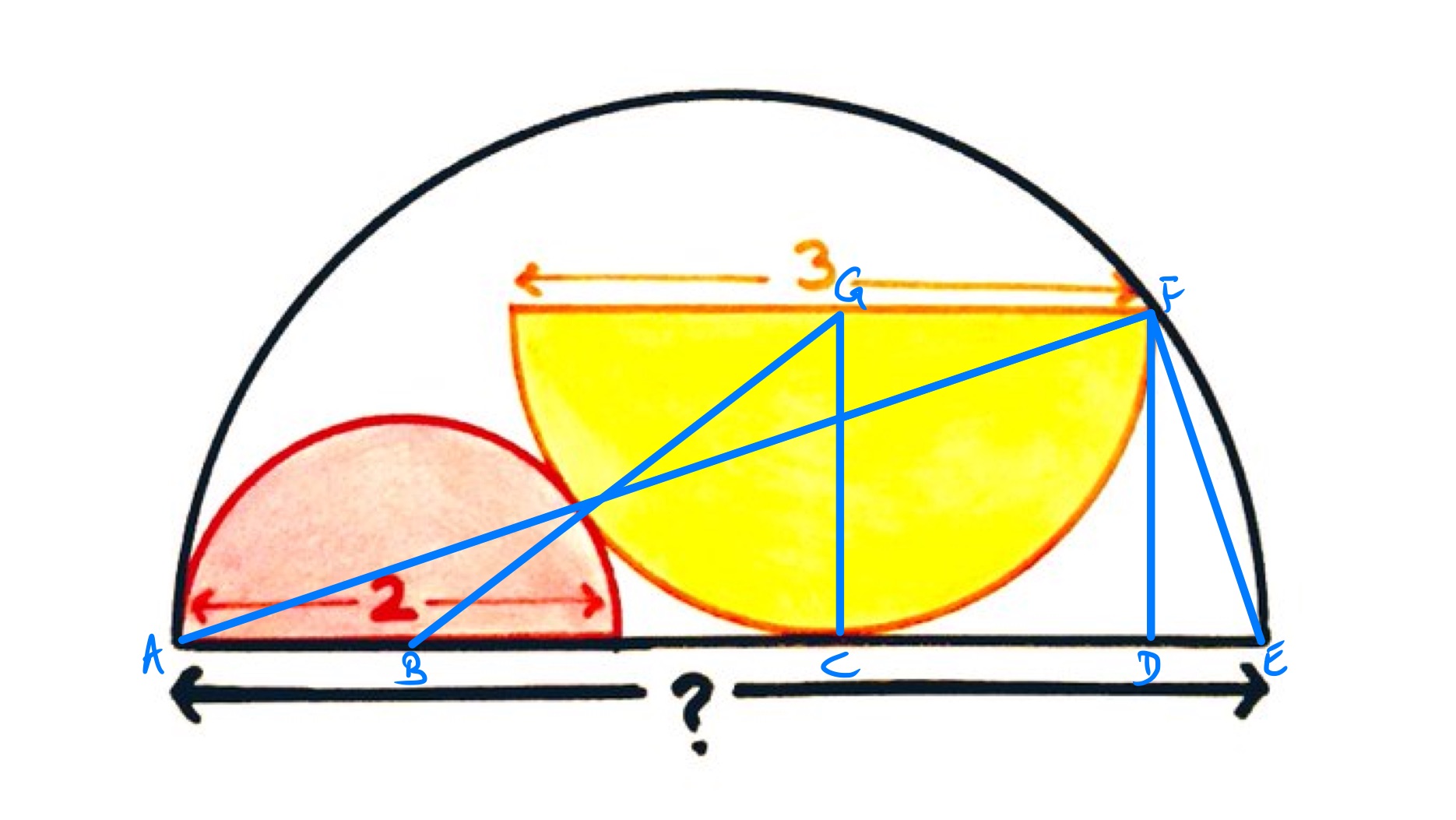
With the points labelled as above, and are the centres of their respective circles and is directly below .
The length of is and of is . As is tangential to the yellow semi-circle at , angle is the angle between a radius and tangent so is a right-angle. Therefore, triangle is a right-angled triangle. Applying Pythagoras' theorem shows that has length . The full length of is then .
Angle is the angle in a semi-circle so is a right-angle. Therefore angles and add up to and so triangles and are similar. As has length and length , the length of is one third of that of and so is . Therefore has length .