Notes
two semi-circles in an equilateral triangle solution
Solution to the Two Semi-Circles In an Equilateral Triangle Puzzle
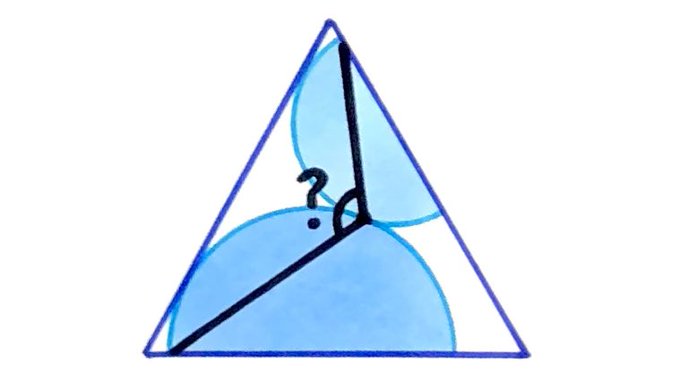
Two semicircles inside an equilateral triangle. What’s the angle?
Solution by Angle Between a Tangent and Radius, Angle at the Circumference is Half the Angle at the Centre, and Angles in a Triangle
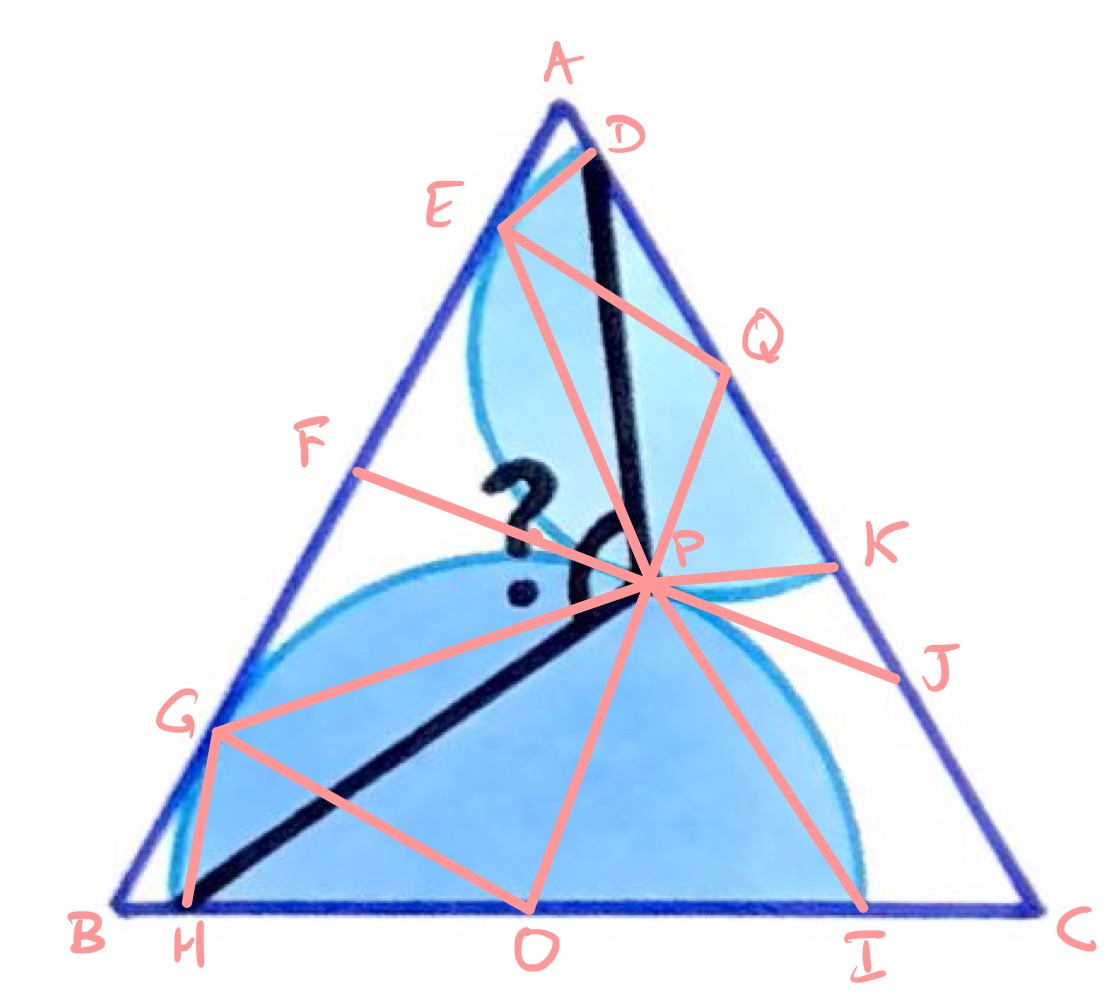
In the diagram above, and are the centres of their respective semi-circles, is the point of tangency and is the tangent to both circles at .
Since the angle between a tangent and radius is , the angles in an equilateral triangle are , and the angles in a triangle add up to , angle is .
Then as the angle at the circumference is half the angle at the centre, angle is .
Similarly, angle is also .
Triangle is isosceles as line segments and are both tangent to the same circle, as is triangle . This means that angle is .
Therefore, angle is .
Angles and a