Notes
two semi-circles in a semi-circle solution
Solution to the Two Semi-Circles in a Semi-Circle Puzzle
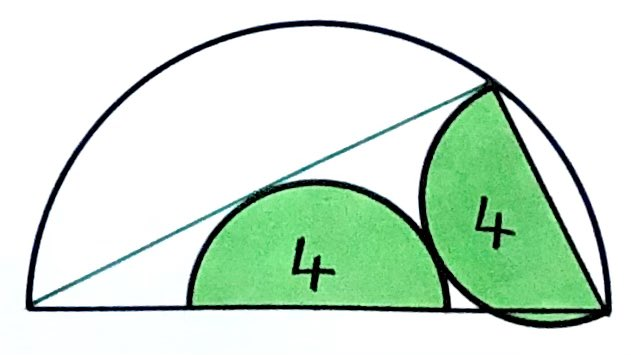
What’s the area of the large semicircle?
Solution by angle in a semi-circle, similar triangles, and Pythagoras' theorem
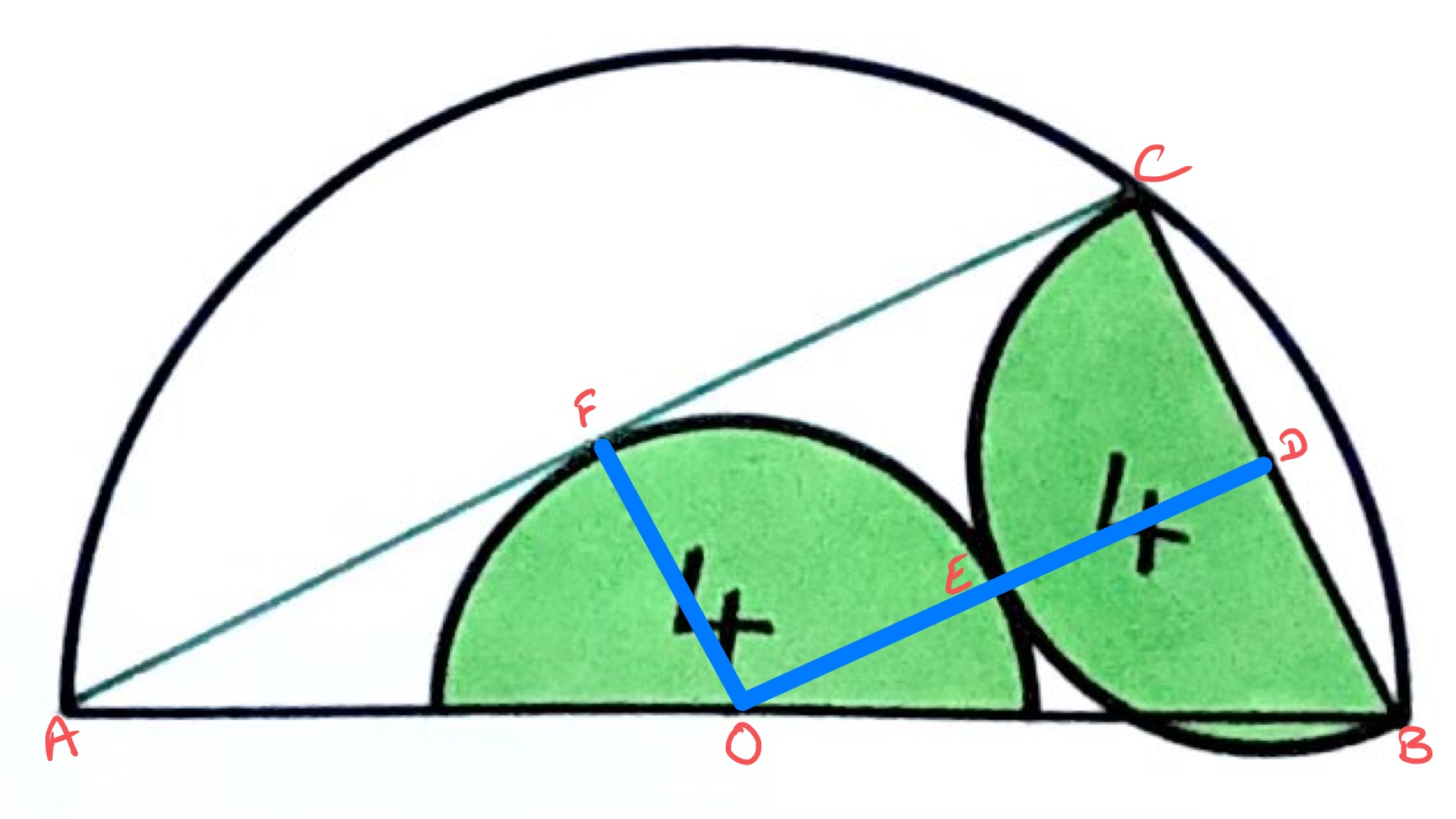
In the above diagram, is the centre of the left-hand green semi-circle and the centre of the right-hand one. The point of contact, , lies on the line .
Angle is a right-angle as it is the angle in a semi-circle. Angle is a right-angle as it is the angle between a radius and tangent. The line segments and are radii of the two semi-circles and so are the same length. The quadrilateral is therefore a rectangle.
The line segment is therefore parallel to and so triangles and are similar. Since is half of , is half of and is therefore a radius of the large semi-circle.
In the triangle , the length of is twice that of , which is a radius of the smaller semi-circle. Applying Pythagoras' theorem to this triangle gives the following relationship between the radii of the semi-circles:
Multiplying this through by shows that the area of the larger semi-circle is times that of the green ones, and so has area .