Notes
two semi-circles in a circle solution
Solution to the Two Semi-Circles in a Circle Puzzle
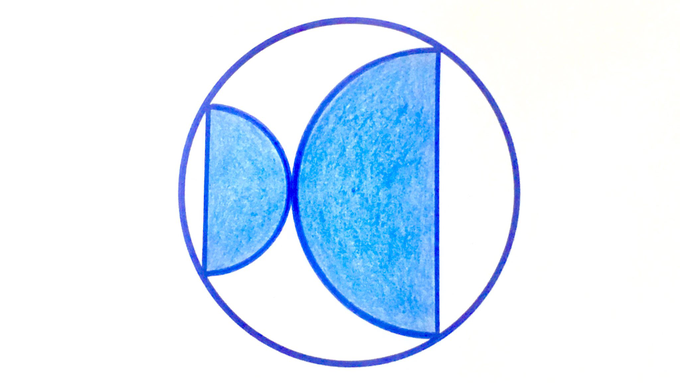
The bases of the semicircles are parallel. What fraction of the circle is shaded?
Solution by Congruent Triangles and Pythagoras' Theorem
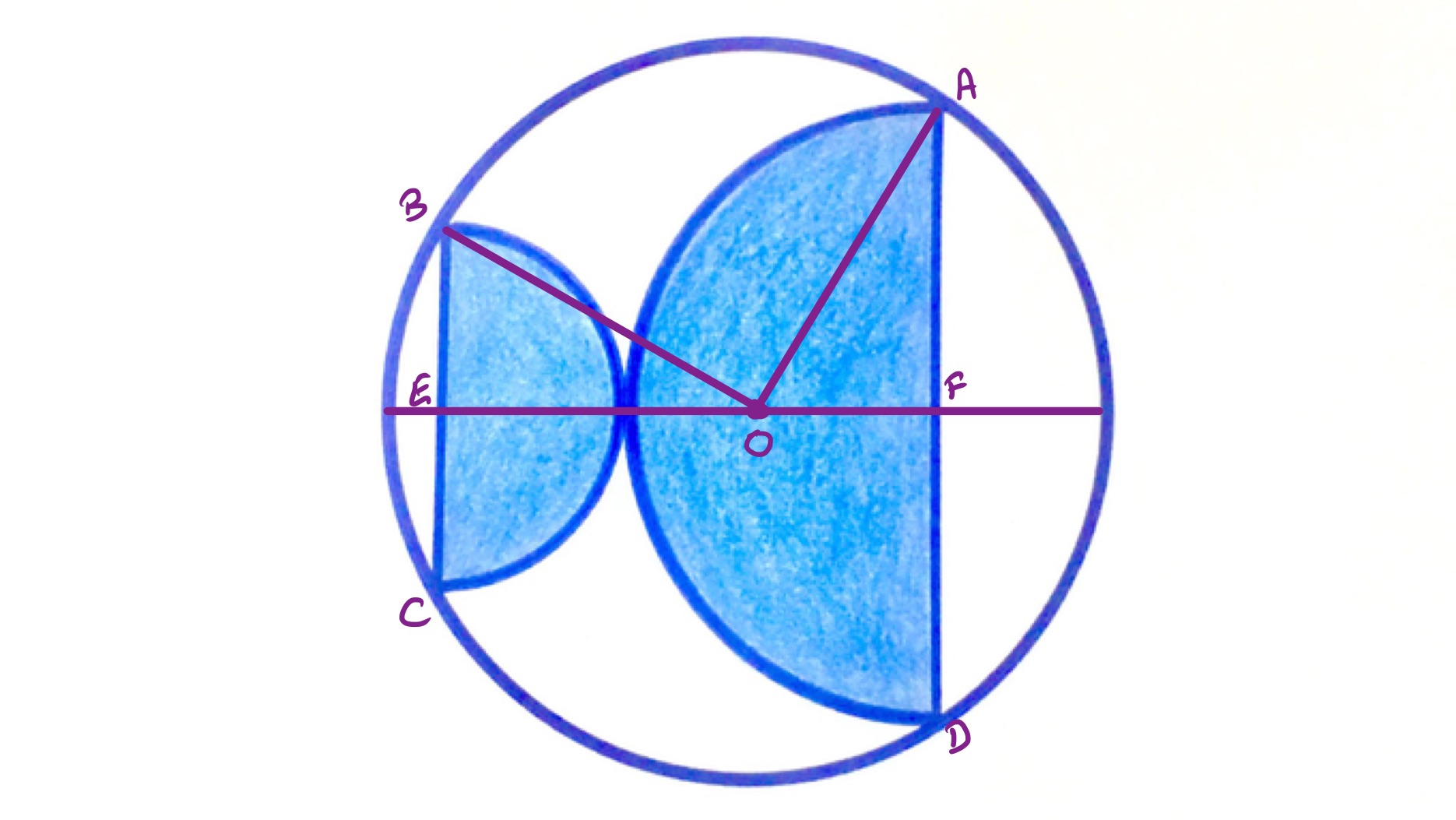
In the above diagram, the points and are midpoints of those chords and the line through and is the perpendicular bisector through those chords so is a diameter of the circle.
The length of is the sum of the lengths of and . Let be the point so that has the same length as , and so has the same length as . Then and are right-angled triangles with the same side lengths adjacent to the right-angles, so are congruent. This means that the lengths of and are the same. As and are on the circumference of the circle and is on a diameter, it is therefore the centre of the circle.
This means that is a radius and has the same length as , so with as the length of , as the length of , and as the length of , Pythagoras' theorem applied to the triangle shows that:
The shaded areas are and the whole circle has area , so the shaded area is of the total circle.
Solution by Midpoints of Chords and Pythagoras' Theorem
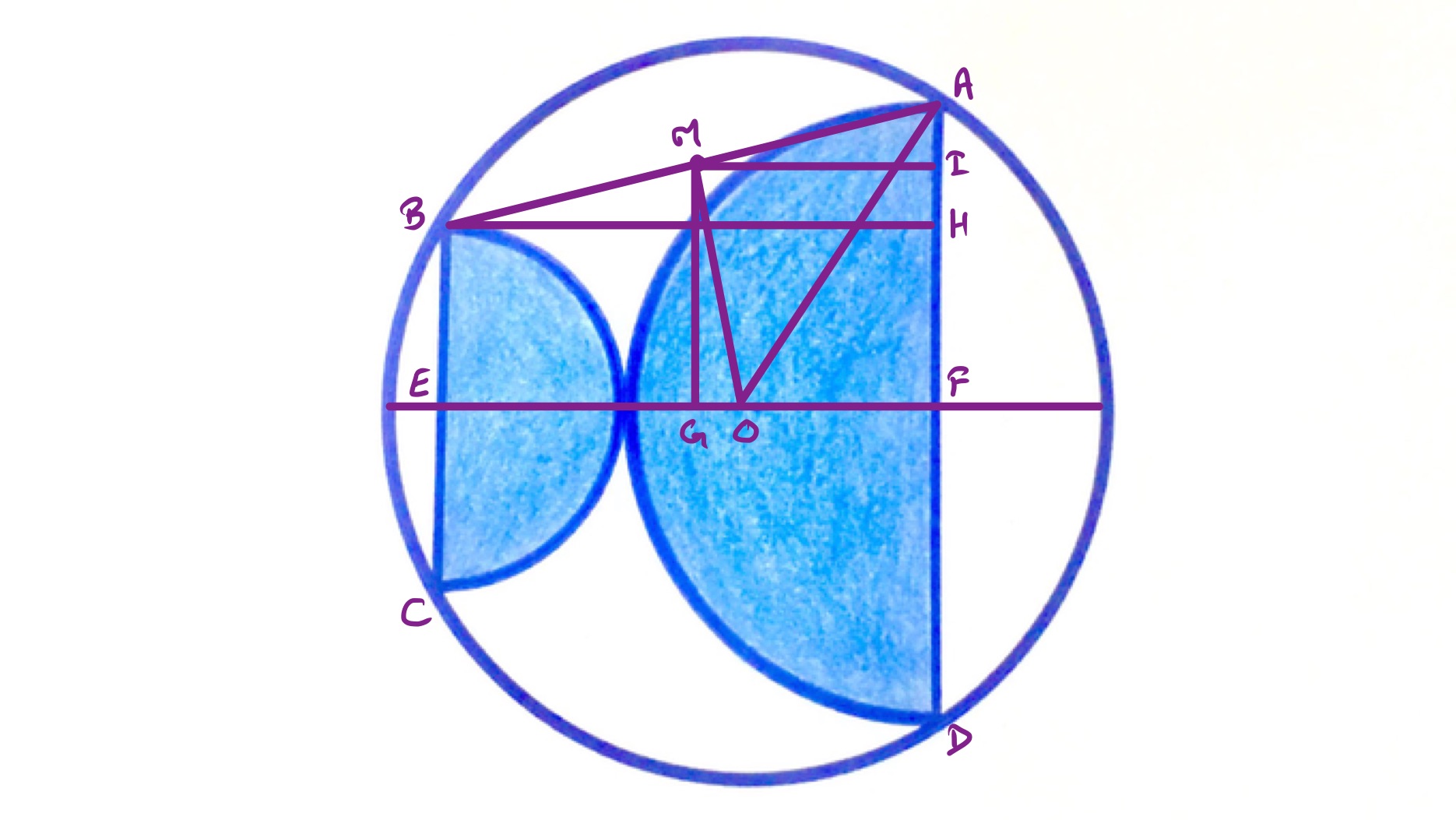
In the above diagram, is the midpoint of the chord , of , and of . The line through and is the perpendicular bisector of each of the chords and and so is a diameter of the circle. The point , which lies on this diameter, is the centre of the circle.
The points , , and are so that is perpendicular to , is perpendicular to , and is also perpendicular to .
As is the midpoint of , is the midpoint of , and so the length is half of the sum of the radii of the two semi-circles. Similarly, is the midpoint of and so the length of is the average of the radii of the two semi-circles. Hence and have the same length. Since angles and are both right-angles, angles and are equal. Therefore, triangles and are congruent.
The length of is therefore the same as that of , which is half the difference of the radii of the smaller circles. Since the length of is half the sum of these radii, is the same length as the smaller radius, namely the length of .
Applying Pythagoras' theorem to triangle then shows that, with and the radii of the semi-circles and of the outer circle,
As above, then, the shaded areas are and the whole circle has area , so the shaded area is of the total circle.
Solution by Invariance Principle
There are two special configurations of this puzzle. In the first, one of the circles is as large as can be and the second is non-existent. In the second, the two circles are of equal size.

In this case, it is clear that the shaded area is half the area of the full circle.
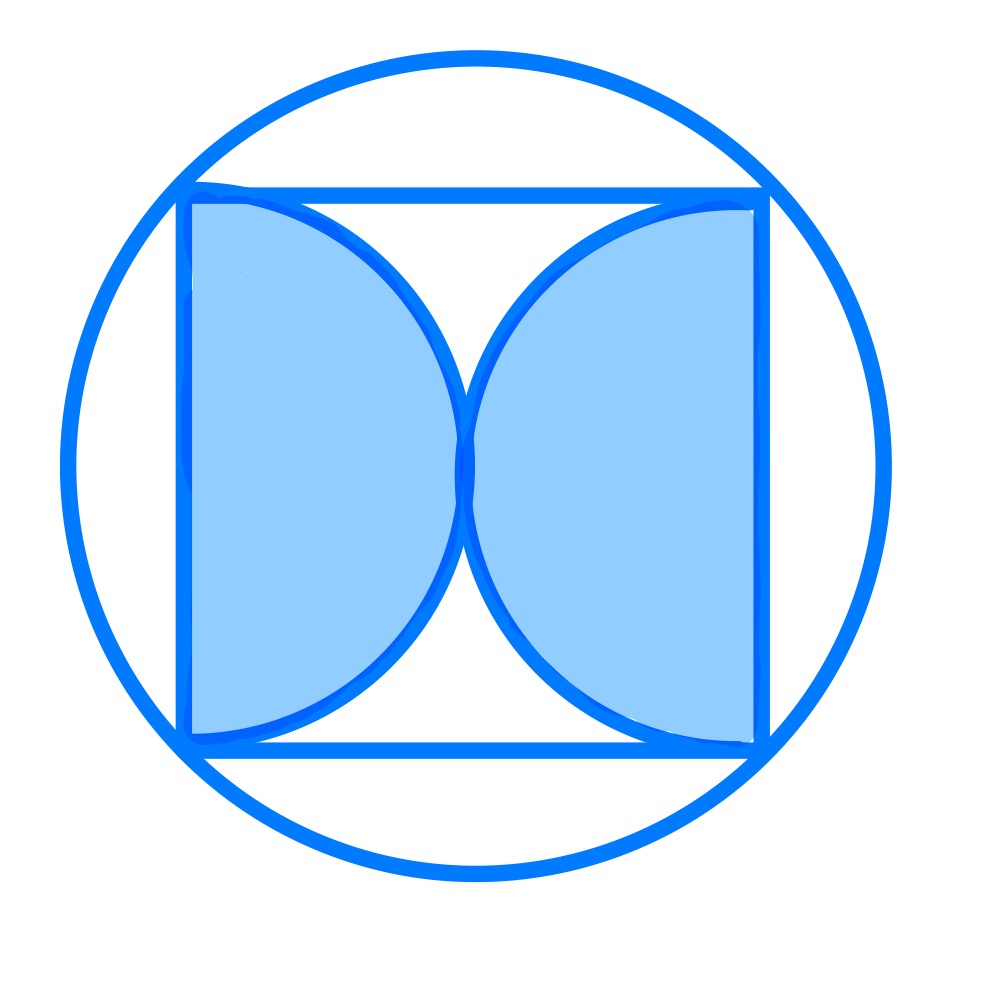
In this case, the diameters of the smaller circles form two sides of a square and the diagonal of this square is then a diameter of the larger circle. Since the length of the diagonal is times the length of a side, the area of the large circle is times the area of the two semi-circles made into a circle.