Notes
two semi-circles diagonally across a square solution
Two Semi-Circles Diagonally Across a Square
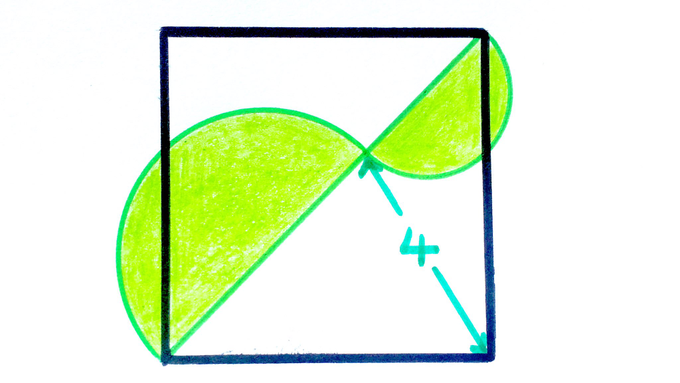
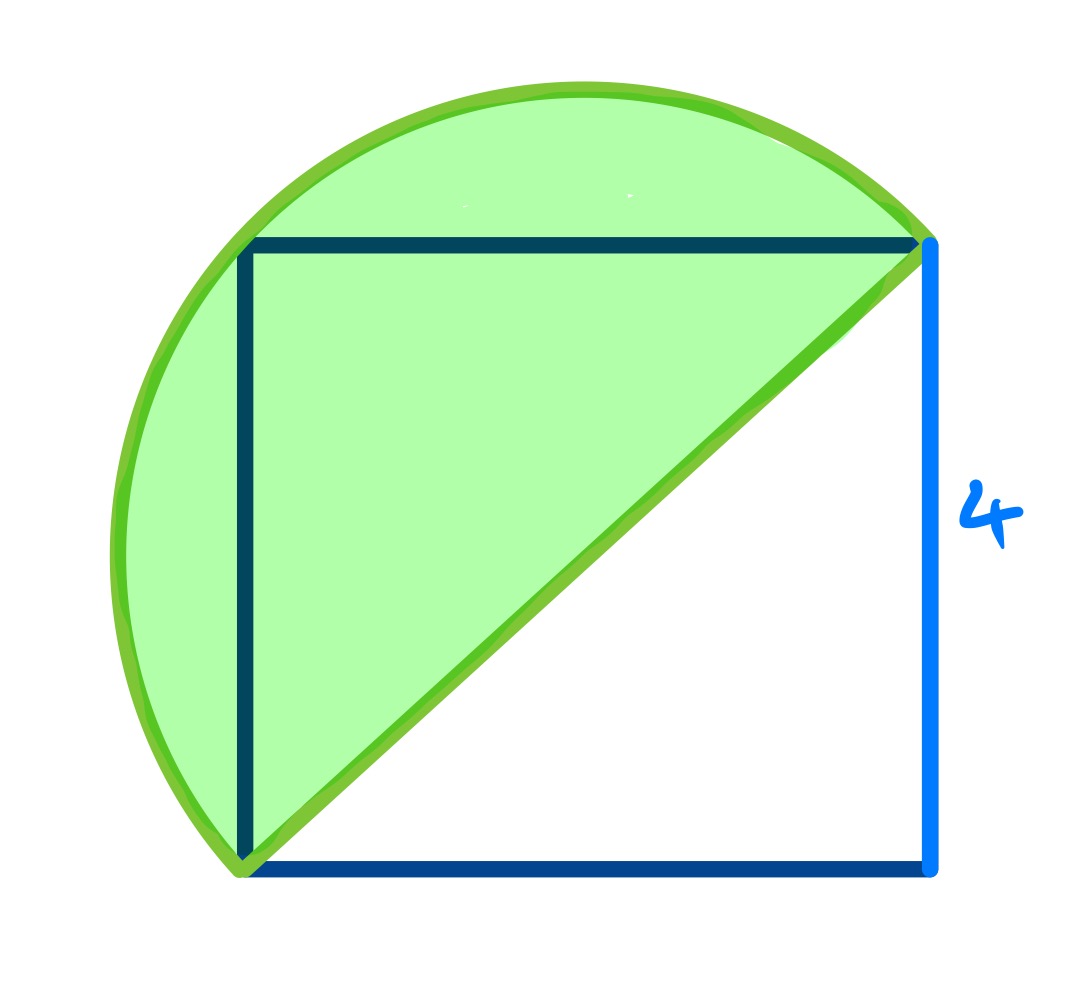
Two semicircles are placed on the diagonal of a square. What’s the total shaded area?
Solution by Pythagoras' Theorem
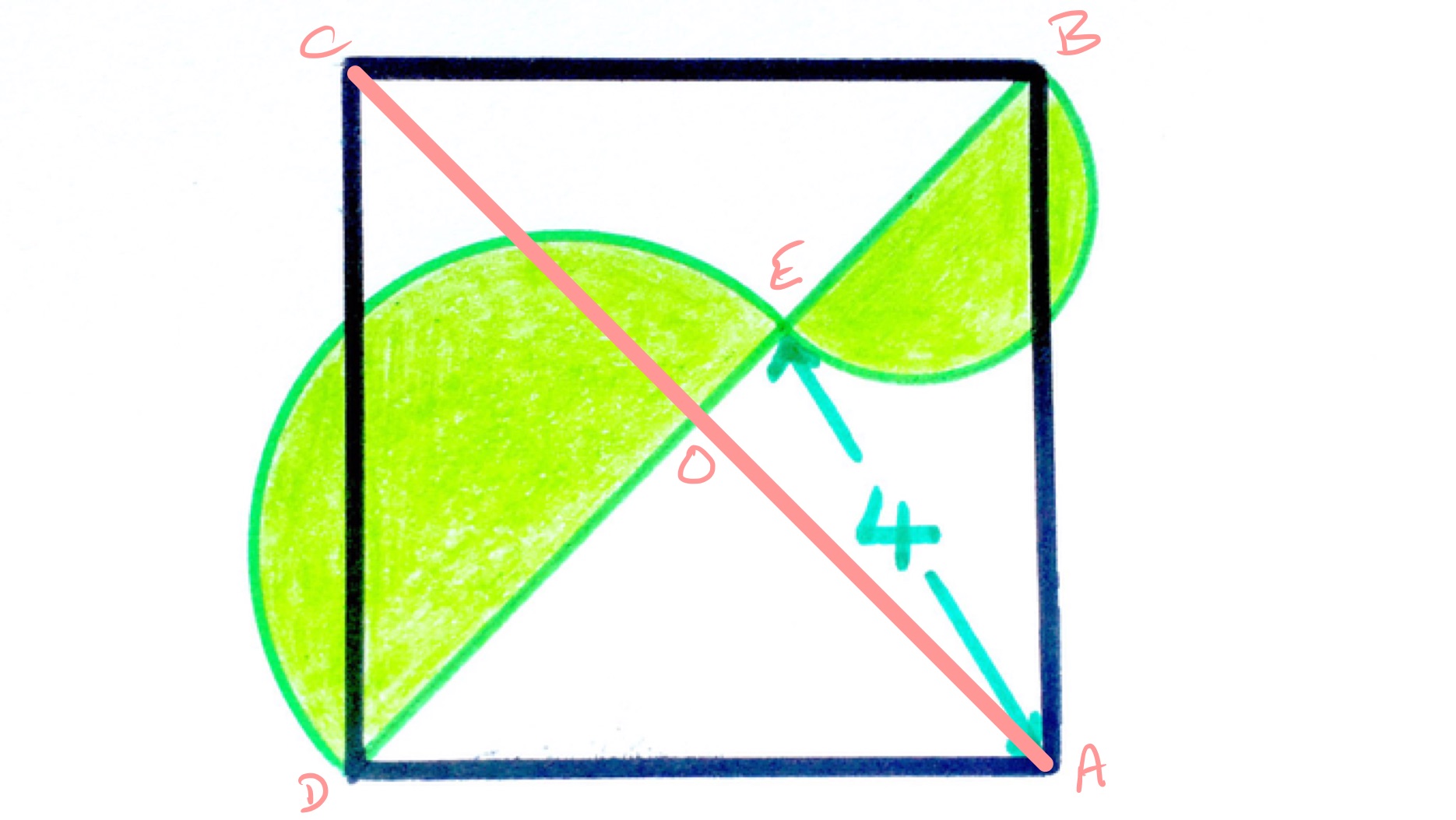
With the points labelled as above, let be the diameter of the lower semi-circle and the diameter of the upper. The total shaded area is then .
Triangle is a right-angled triangle. The full diagonal of the square is then , so the length of is . The length of is . Applying Pythagoras' Theorem to triangle yields the equation:
The left-hand side expands to
So the shaded area is:
Solution by Invariance Principle
The relative sizes of the semi-circles can be varied. In the first special case, the two are the same size, so the half diagonal of the square is of length and this is also the diameters of the semi-circles. This gives an area of .
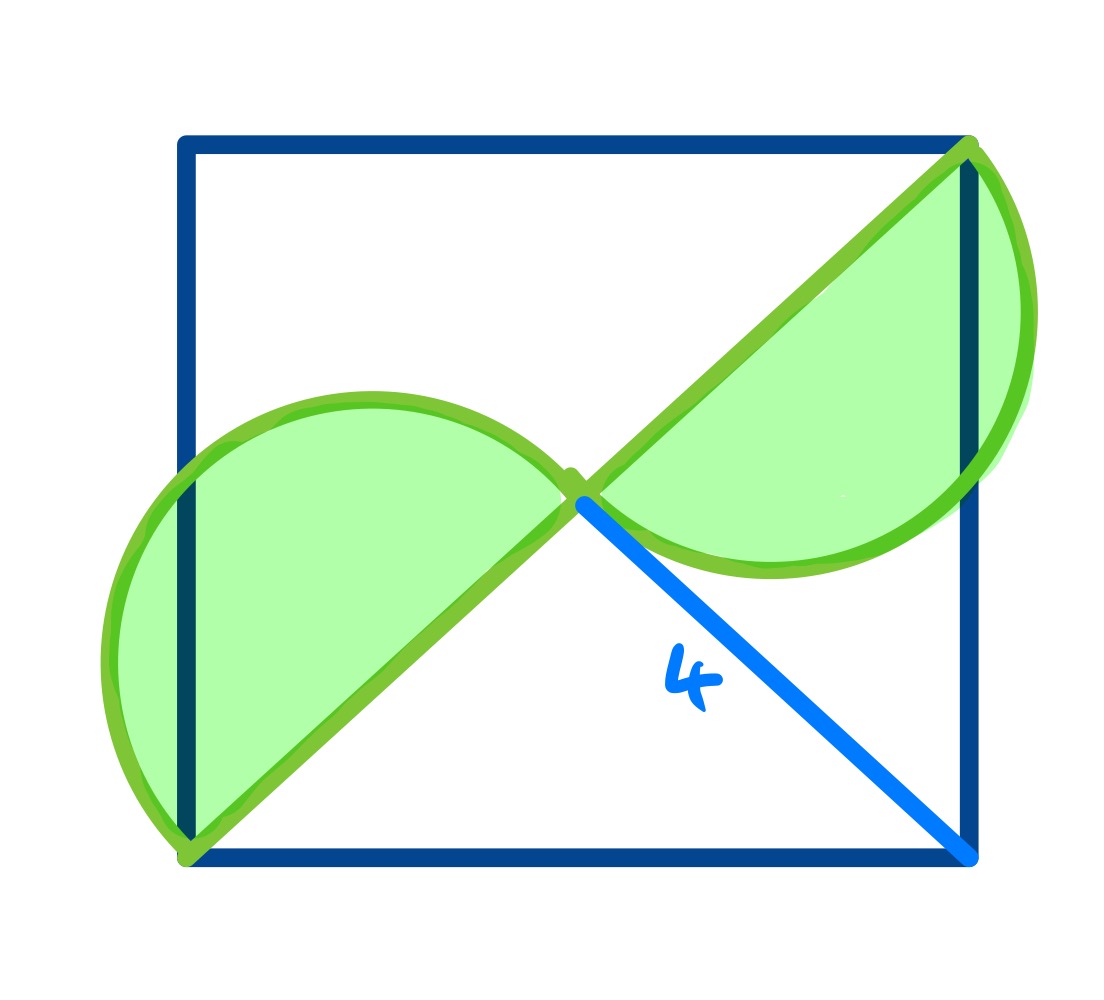
In the second special case, the lower semi-circle is as large as it can be and the upper as small. This means that the diameter of the lower semi-circle is the diagonal of the square and the side of the square is of length . The diagonal is therefore and the area of the semi-circle is .