Notes
two semi-circles and two quarter circles solution
Solution to the Two Semi-Circles and Two Quarter Circles Puzzle
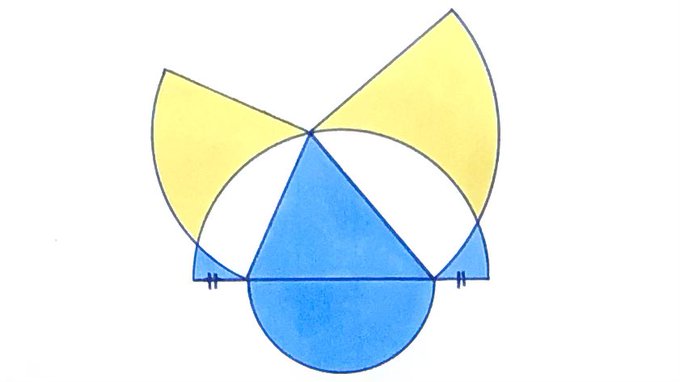
This design is made from two semicircles and two quarter circles. Is more of it shaded yellow or blue?
Solution by Pythagoras' Theorem and the Area of a Circle
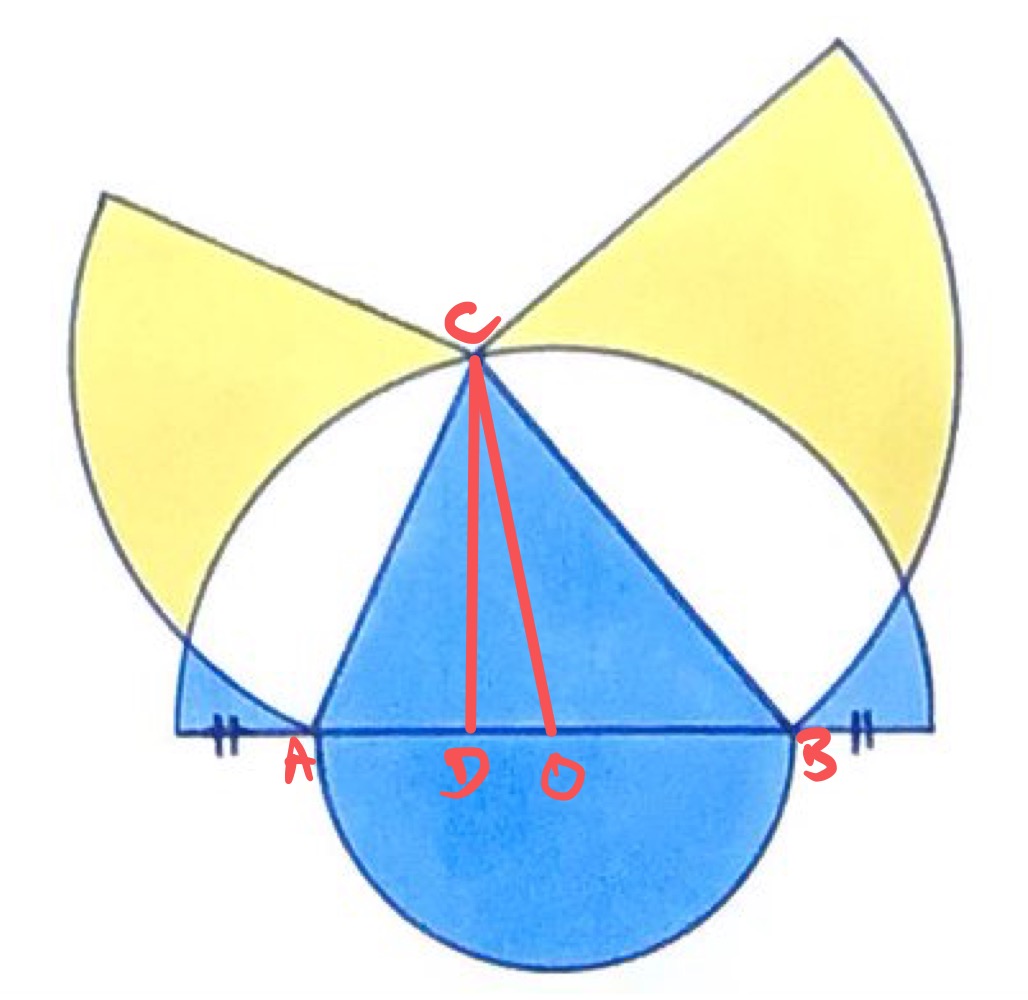
In the above diagram, is the centre of the two semi-circles and is such that angle is a right-angle.
By including the white regions to both the yellow and blue, the comparison is between the two quarter circles and the two semi-circles.
Let be the radius of the larger blue semi-circle and of the smaller. Let be the radius of the left quarter circle and of the right. So the sides of the blue triangle are , , and . Let be the length of the line segment and of .
There are three right-angled triangles, namely , , and . Applying Pythagoras' theorem to all three yields:
Adding the first two equations together gives:
And then substituting in the third shows that .
Multiplying by gives:
and so the blue and yellow regions have the same area.
Solution by the Cosine Rule and Parallelogram Identity
The above can be shortened by using either the cosine rule or the parallelogram identity.
Using the cosine rule avoids needing point . Applied to triangles and it yields:
\begin{aligned}
a^2 &= r^2 + R^2 - 2 r R \cos( B \hat{O} C) \\
b^2 &= r^2 + R^2 - 2 r R \cos( C \hat{O} A)
\begin{aligned}
Then, since , adding the equations gives:
This is also the result of applying the parallelogram identity to the parallelogram obtained by duplicating triangle and rotating it about (so that as a diameter).
Solution by Invariance Principle
The positions of point on the circumference and and on the diameter can be varied, leading to two positions where the result is obvious. In both, is positioned at the midpoint of the arc.
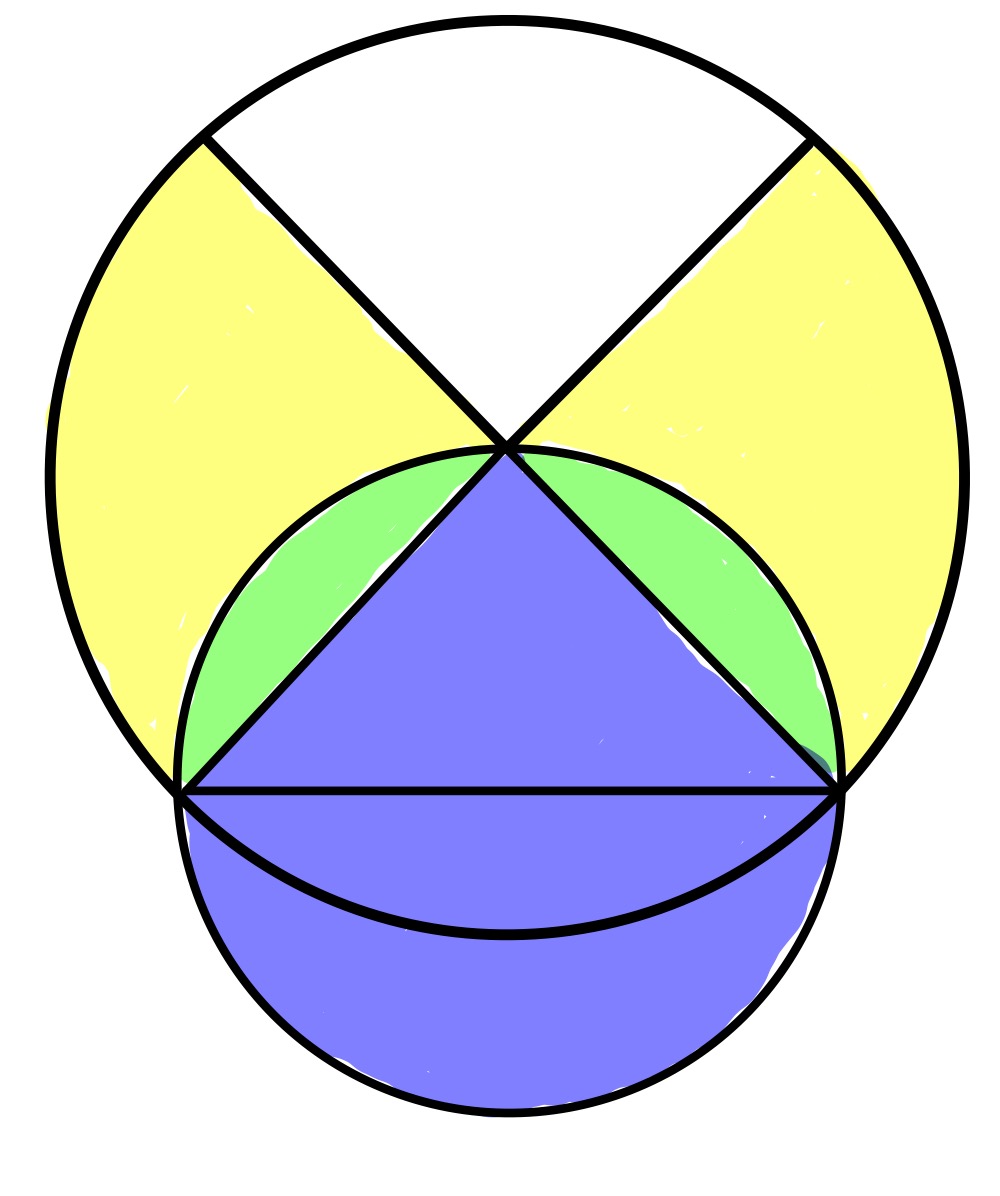
Here, and are at the ends of the diameter, meaning that the blue and green is a full circle. The triangle is an isosceles right-angled triangle so its sides are in the ratio . So the yellow and green regions comprise half a circle of twice the area of the blue and green.
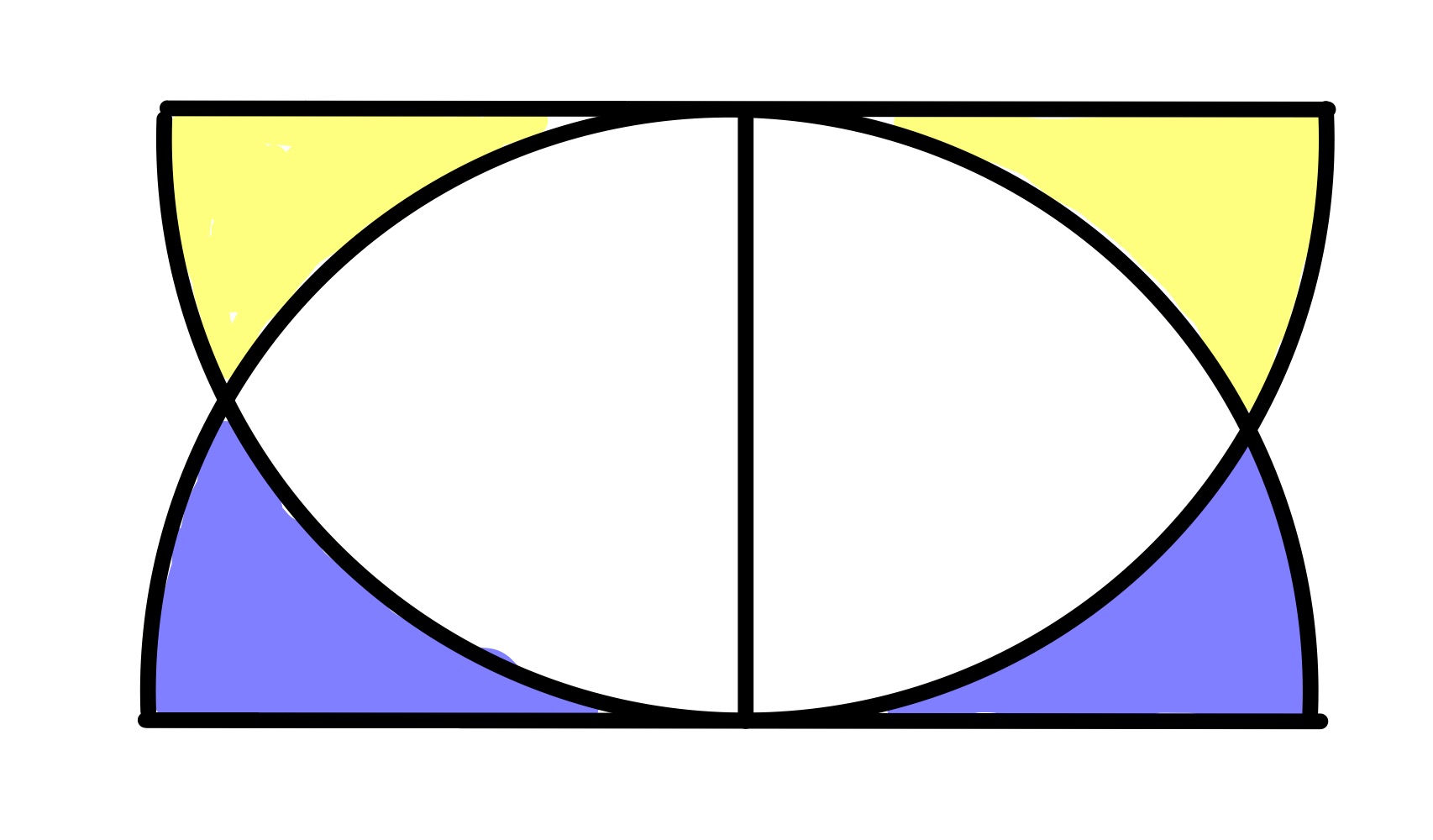
Here, and are at the centre of the blue semi-circle, and the yellow quarter circles combine to be a semi-circle of exactly the same size.