Notes
two semi-circles and an equilateral triangle solution
Solution to the Two Semi-Circles and an Equilateral Triangle Puzzle
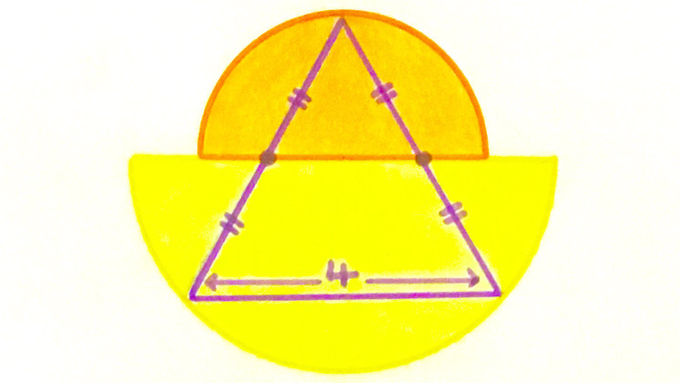
The triangle is equilateral. What’s the total area of the two semicircles?
Solution by Pythagoras' Theorem and Lengths in Equilateral Triangles
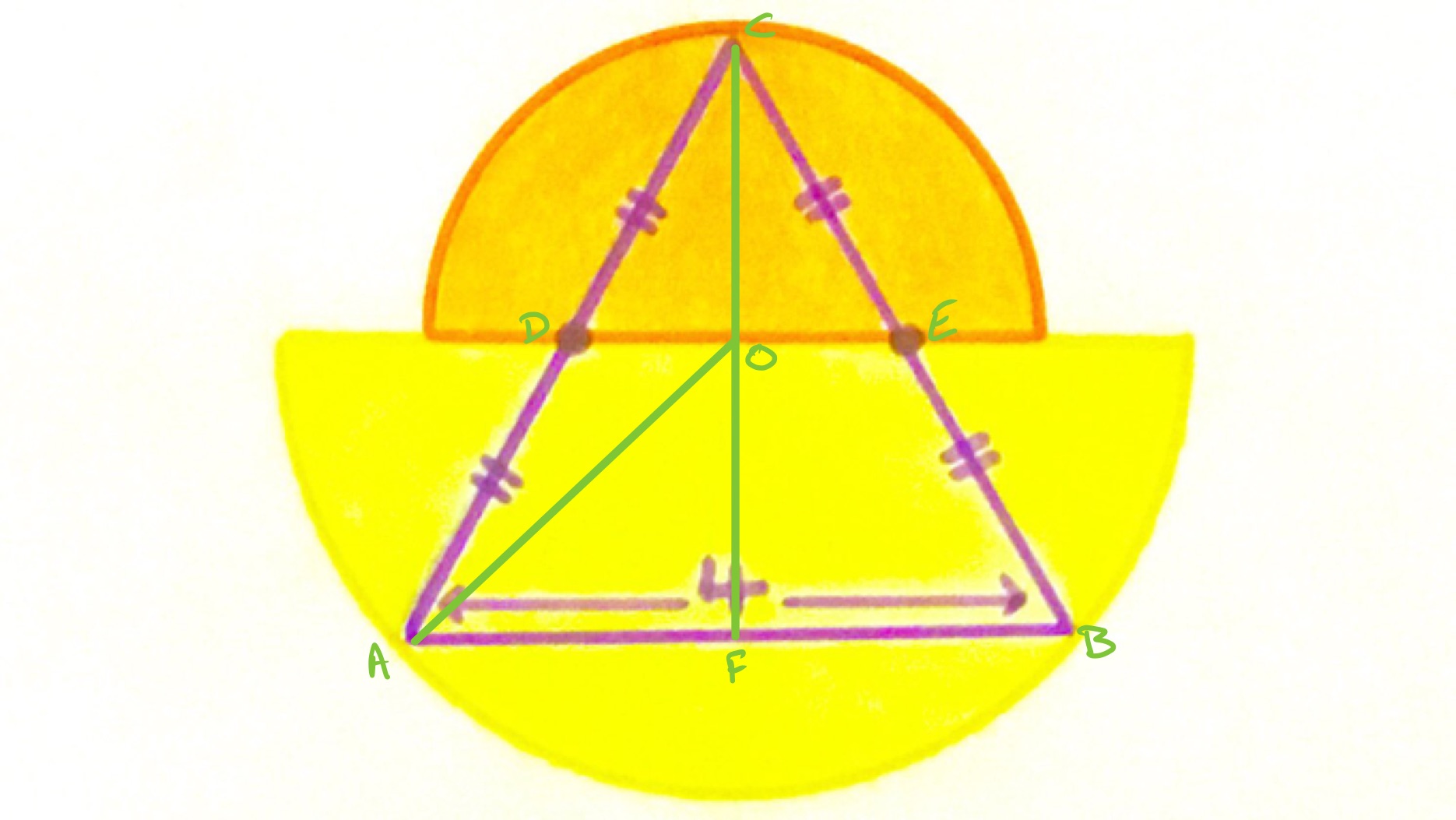
In the above diagram, point is the centre of the semi-circles. As the diameters of the semi-circles cut the triangle halfway along the two sides, is the midpoint of . As the triangle is equilateral, has length so has length and then has length . So the area of the orange semi-circle is .
Then is a right-angled triangle with of length and of length , so by Pythagoras' theorem, has length . The yellow triangle therefore has area .
The total are of the two semi-circles is then .