Notes
two rectangles with diagonals solution
Solution to the Two Rectangles with Diagonals Puzzle
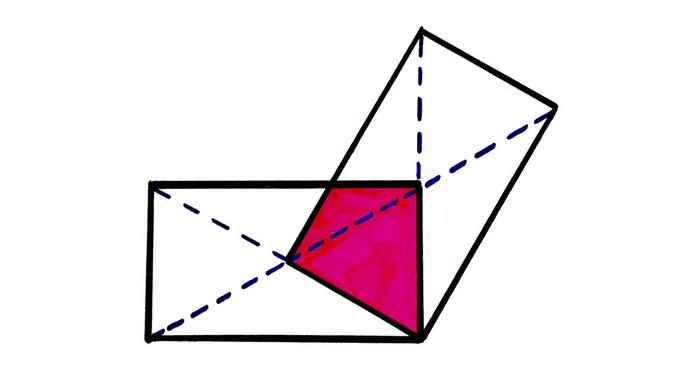
Two rectangles and their diagonals. What fraction of the total area is shaded?
Solution by Similar Triangles and Equilateral Triangles
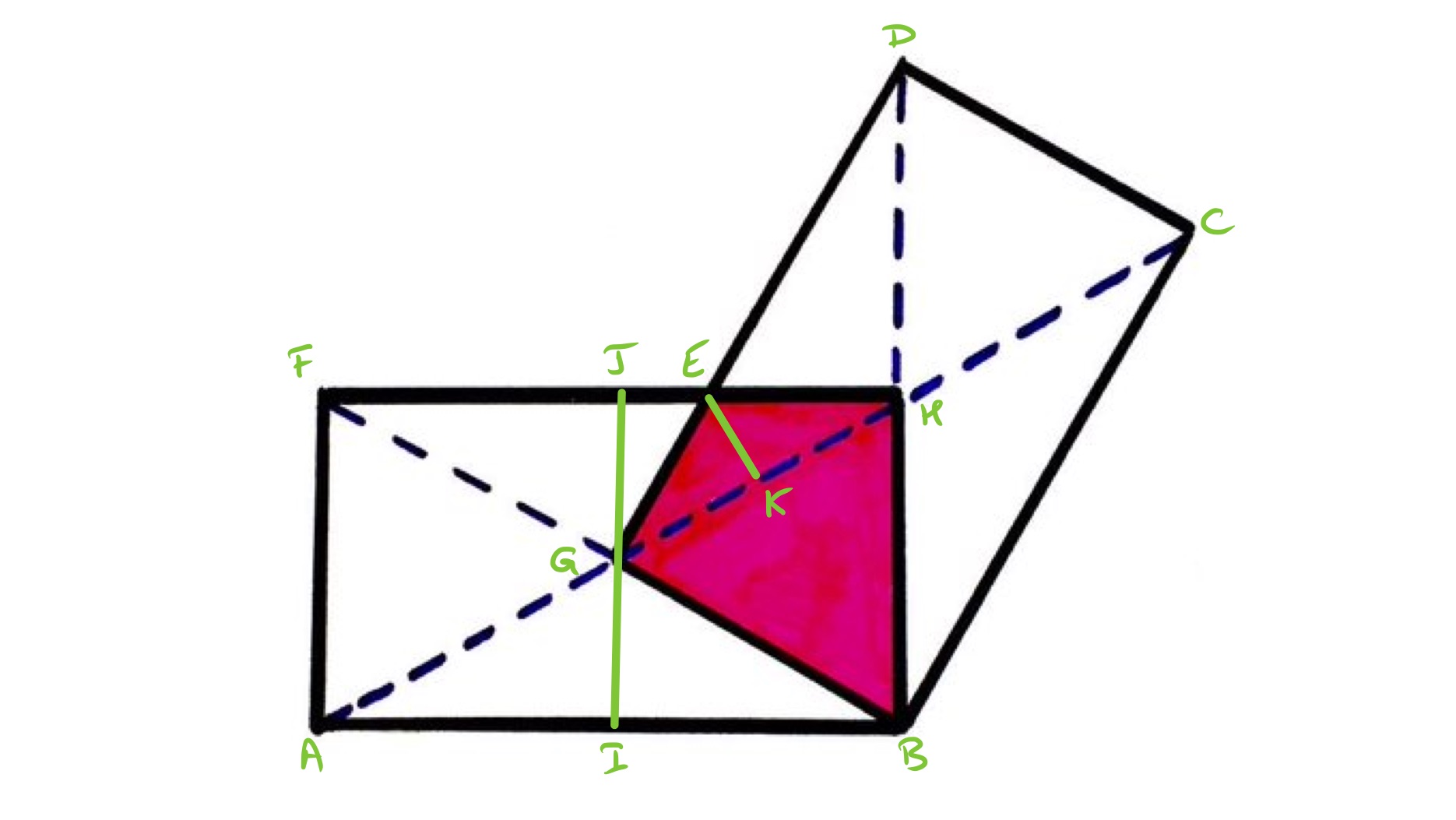
First, note that the rectangles are similar since the angle between a side and the diagonal is the same for each (angle ). So the ratio of the side to the half-diagonal is the same for each, so the ratio of the lengths of to is the same as with them the other way round, which means that they must be equal in length. This is also the length of so triangle is equilateral and quadrilateral is a kite.
Since triangle is equilateral, triangle is half an equilateral triangle of the same side length. Each rectangle therefore has area four times that of the triangle .
Triangle is then half of an equilateral triangle, so has double the length of . The point is the midpoint of so is the same length as and triangles and are congruent. Triangle is therefore two thirds of and so its area is one third of that of . The area of the purple region is therefore rds of the area of .
The total area is then times the area of , so the fraction that is shaded is th of the total area.